Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8 ha. Trên diện tích mỗi ha, nếu trồng dứa thì cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu ha để thu được nhiều tiền nhất, biết rằng tổng số công không quá 180.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8 ha. Trên diện tích mỗi ha, nếu trồng dứa thì cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu ha để thu được nhiều tiền nhất, biết rằng tổng số công không quá 180.
Quảng cáo
Trả lời:
Gọi \(x,y\) lần lượt là số ha trồng dứa và củ đậu. Điều kiện: . Tổng diện tích trồng là \(x + y\) (ha); tổng số công cần thiết là \(20x + 30y\) (công). Số tiền thu được là \(T(x,y) = 3x + 4y\)
Ta có hệ bất phương trình
Miền nghiệm của hệ \((*)\) là miền tứ giác \(OABC\) (kề cả biên) với \(O(0;0)A(0;6),B(6;2),C(0;8)\)
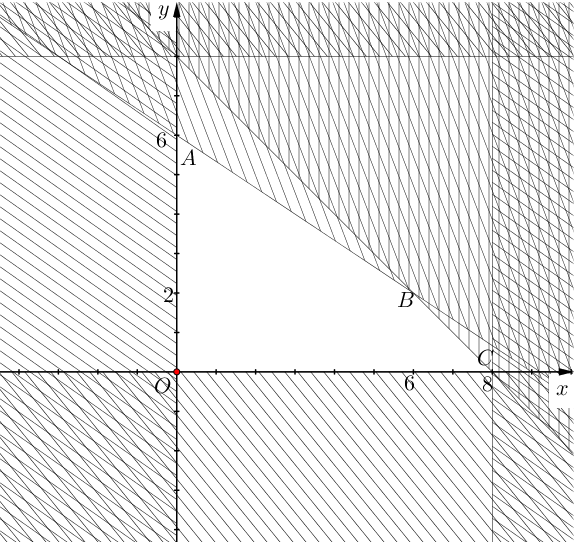
Khi đó \(T(x,y)\) đạt cực đại tại một trong các đỉnh của tứ giác \(OABC\).
Ta có: \(T(0,0) = 0;T(0;6) = 24;T(6;2) = 26;T(8;0) = 24\).
Vậy giá trị lớn nhất của \(T(x,y)\) bằng 26 (triệu đồng), khi đó \(x = 6,y = 2\) (tức là hộ nông dân cần trồng \(6ha\) dứa và \(2ha\) củ đậu để có thể thu lại số tiền nhiều nhất).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Miền nghiệm của hệ (I) là miền tứ giác \(ABCD\) với \(A(3;0),B(5;1),C(1;5),D(1;3)\) (Hình).
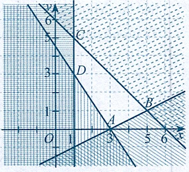
b) \((3;2)\) là một nghiệm của hệ bất phương trình
c) Tính giá trị của \(F = 3x - y\) tại các cặp số \((x;y)\) là toạ độ của các đỉnh tứ giác \(ABCD\) rồi so sánh các giá trị đó, ta được \(F\) đạt giá trị lớn nhất bằng 14 tại \(x = 5,y = 1\)
d) \(F\) đạt giá trị nhỏ nhất bằng \( - 2\) tại \(x = 1,y = 5\).
Lời giải
|
a) Đúng |
b) Sai |
c) Sai |
d) Đúng |
a) Gọi \(x,y\) (đơn vị: triệu đồng) tiền bác Minh đầu tư vào kho Ta có hệ bất phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{x + y \le 240}\\{y \ge 40}\\{x \ge 3y}\end{array}} \right.\)
b) Miền nghiệm của hệ trên là miền tam giác \(ABC\) với \(A(180;60),B(120;40)\), \(C(200;40)\) ở Hình.
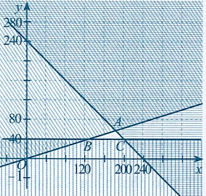
c) Điểm \(C(200;40)\) thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho
d) Điểm \(A(180;60)\) là điểm có tung độ lớn nhất thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.