Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một trò chơi chọn ô chữ đơn giản mà kết quả gồm một trong hai khả năng: Nếu người chơi chọn được chữ \(A\) thì người ấy được cộng 3 điểm, nếu người chơi chọn được chữ \(B\) thì người ấy bị trừ 1 điểm. Người chơi chỉ chiến thắng khi đạt được số điểm tối thiểu là 20. Gọi \(x,y\) theo thứ tự là số lần người chơi chọn được chữ \(A\) và chữ \(B\). Khi đó:
a) Tổng số điểm người chơi đạt được khi chọn chữ \(A\) là \(3x\), tổng số điểm người chơi bị trừ khi chọn chữ \(B\) là \(y\).
b) Bất phương trình bậc nhất hai ẩn \(x,y\) trong tình huống người chơi chiến thắng là
c) Người chơi chọn được chữ \(A\) 7 lần và chọn được chữ \(B\) 1 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
d) Người chơi chọn được chữ \(A\) 8 lần và chọn được chữ \(B\) 3 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một trò chơi chọn ô chữ đơn giản mà kết quả gồm một trong hai khả năng: Nếu người chơi chọn được chữ \(A\) thì người ấy được cộng 3 điểm, nếu người chơi chọn được chữ \(B\) thì người ấy bị trừ 1 điểm. Người chơi chỉ chiến thắng khi đạt được số điểm tối thiểu là 20. Gọi \(x,y\) theo thứ tự là số lần người chơi chọn được chữ \(A\) và chữ \(B\). Khi đó:
a) Tổng số điểm người chơi đạt được khi chọn chữ \(A\) là \(3x\), tổng số điểm người chơi bị trừ khi chọn chữ \(B\) là \(y\).
b) Bất phương trình bậc nhất hai ẩn \(x,y\) trong tình huống người chơi chiến thắng là
c) Người chơi chọn được chữ \(A\) 7 lần và chọn được chữ \(B\) 1 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
d) Người chơi chọn được chữ \(A\) 8 lần và chọn được chữ \(B\) 3 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
Câu hỏi trong đề: Đề kiểm tra Bài tập cuối chương II (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
a) Đúng |
b) Sai |
c) Đúng |
d) Sai |
a) Tổng số điểm người chơi đạt được khi chọn chữ \(A\) là \(3x\), tổng số điểm người chơi bị trừ khi chọn chữ \(B\) là \(y\).
b) Với \(x,y \in \mathbb{N}\), ta có bất phương trình: .
c) Thay cặp số \((7;1)\) vào bất phương trình (đúng), suy ra \((7;1)\) là một nghiệm của \((*)\). Điều này cho thấy nếu người chơi chọn được chữ \(A\) 7 lần và chọn được chữ \(B\) 1 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
d) Thay cặp số \((8;4)\) vào bất phương trình (đúng), suy ra \((8;4)\) là một nghiệm của \((*)\). Điều này cho thấy nếu người chơi chọn được chữ \(A\) 8 lần và chọn được chữ \(B\) 4 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đường thẳng \(AB:\frac{{x - 0}}{{ - 1 - 0}} = \frac{{y - 3}}{{2 - 3}} \Leftrightarrow x - y + 3 = 0\).
Đường thẳng \(AC:\frac{{x - 0}}{{2 - 0}} = \frac{{y - 3}}{{1 - 3}} \Leftrightarrow x + y - 3 = 0\).
Đường thẳng \(BC:\frac{{x - 2}}{{2 - ( - 1)}} = \frac{{y - 1}}{{1 - 2}} \Leftrightarrow x + 3y - 5 = 0\).
Điều kiện cần và đủ để điểm \(M\) nằm bên trong tam giác \(ABC\) là điểm \(M\) cùng với mỗi đỉnh \(A,B,C\) lần lượt cùng phía với nhau đối với cạnh \(AB,AC,BC\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}(1 \cdot 0 + 3 \cdot 3 - 5) \cdot (1 \cdot m + 3 \cdot \frac{{2m - 1}}{2} - 5) > 0\\(1 \cdot ( - 1) + 1 \cdot 2 - 3) \cdot (1 \cdot m + 1 \cdot \frac{{2m - 1}}{2} - 3) > 0\\(1.2 - 1.1 + 3) \cdot (1 \cdot m - 1 \cdot \frac{{2m - 1}}{2} + 3) > 0\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m > \frac{{13}}{8}\\m < \frac{7}{4}\\14 > 0(tm)\end{array}\end{array} \Leftrightarrow \frac{{13}}{8} < m < \frac{7}{4}} \right.} \right.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Do \(x > 0,\frac{x}{2} + \frac{y}{3} - 1 \le 0\) nên ta có \(\frac{y}{3} < 1 \Leftrightarrow y < 3\)
Do \(y\) nguyên dương nên \(y \in \{ 1;2\} \).
Với \(y = 1\), ta có \(\left\{ {\begin{array}{*{20}{l}}{\frac{x}{2} + \frac{1}{3} - 1 \le 0}\\{x > 0}\end{array} \Leftrightarrow 0 < x \le \frac{4}{3} \Leftrightarrow x = 1} \right.\).
Với \(y = 2\), ta có \(\left\{ {\begin{array}{*{20}{l}}{\frac{x}{2} + \frac{2}{3} - 1 \le 0}\\{x > 0}\end{array} \Leftrightarrow 0 < x \le \frac{2}{3} \Leftrightarrow x \in \emptyset } \right.\).
Vậy bất phương trình \(\frac{x}{2} + \frac{y}{3} - 1 \le 0\) có nghiệm nguyên dương là \((1;1)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
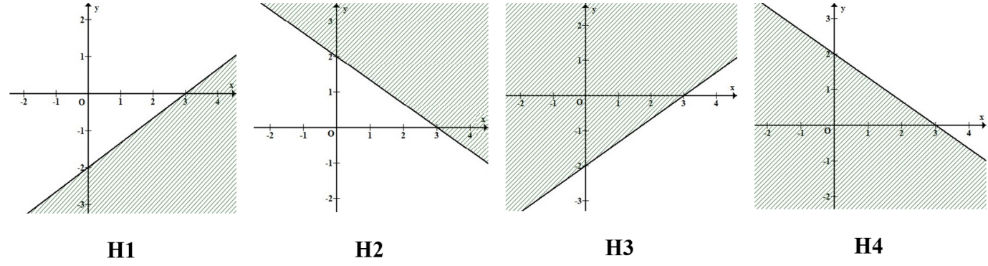
A. H1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left( { - 2\,;\,2} \right) \in S\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập