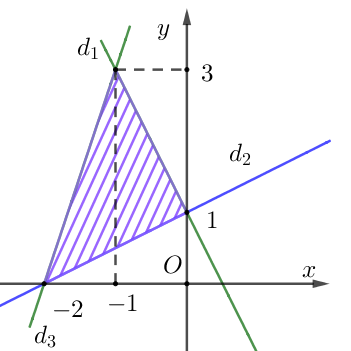
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x + y > 0\\x + 5y - 1 < 0\end{array} \right.\) có tập nghiệm là \(S\). Điểm nào sau đây thuộc tập .
Câu hỏi trong đề: Đề kiểm tra Bài tập cuối chương II (có lời giải) !!
Quảng cáo
Trả lời:
Chọn C
Cách 1:
Ta có biểu diễn miền nghiệm của hệ
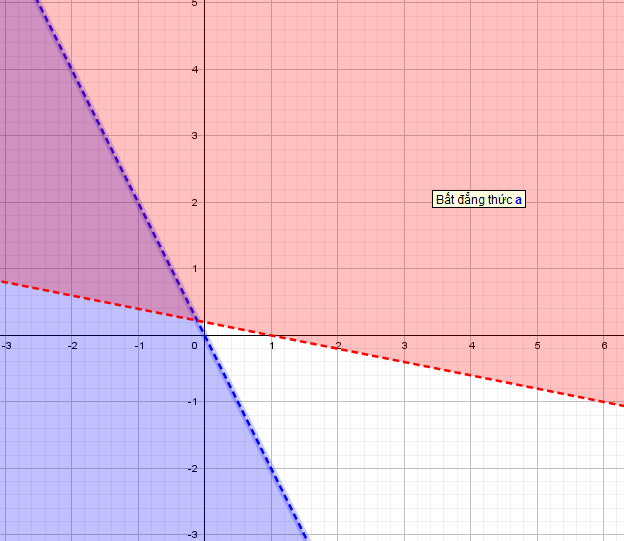
Từ biểu diễn miền nghiệm của hệ ta suy ra Chọn C
Cách 2:
Ta thay lần lượt giá trị của x và y vào hệ để kiểm tra:
\(x = 3;y = - 1\)thì\(\left\{ \begin{array}{l}2x + y > 0\\x + 5y - 1 < 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2x + y = 5 > 0\\x + 5y - 1 = - 2 < 0\end{array} \right.\) thỏa mãn vậy chọn C
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Điều kiện: \(0 \le x \le 2;0 \le y \le 1,5\)
Khi đó số protein có được là \(800x + 600y\) và số lipit có được là \(200x + 400y\)
Vì gia đình đó cần ít nhất 1200 đơn vị protein và 800 đơn vị lipit trong thức ăn mỗi ngày nên điều kiện tương ứng là:
\(800x + 600y \ge 1200 \Leftrightarrow 4x + 3y \ge 6{\rm{ v\`a }}200x + 400y \ge 800 \Leftrightarrow x + 2y \ge 4\)
Ta có hệ bất phương trình sau:
\(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 2}\\{0 \le y \le 1,5}\\{4x + 3y \ge 6}\\{x + 2y \ge 4}\end{array}} \right.\)(*)
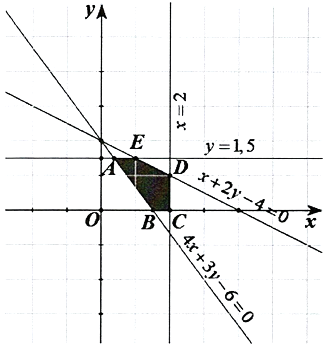
Miền nghiệm của hệ trên là miền ngũ giác \(ABCDE\) kể cả các cạnh của ngũ giác.
Chi phí để mua \(x\;kg\) thịt bò và \(y\;kg\) thịt lợn là \(T = 200x + 100y\) (nghìn đồng).
Bài toán trở thành tìm giá trị nhỏ nhất của \(T(x;y) = 200x + 100y\) trên miền nghiệm của hệ \((*)\).
Tìm tọa độ các điểm \(A,B,C,D,E\).
Tọa độ điểm \(A\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{4x + 5y - 6 = 0}\\{y = \frac{3}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{3}{8}}\\{y = \frac{3}{2}}\end{array}} \right.} \right.\). Vậy \(A\left( {\frac{3}{8};\frac{3}{2}} \right)\).
Tọa độ điềm \(C\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 0}\end{array}} \right.\). Vậy \(C(2;0)\).
Tọa độ điểm \(D\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{x + 2y - 4 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 1}\end{array}} \right.} \right.\). Vậy \(D(2;1)\).
Tọa độ điểm \(E\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x + 2y - 4 = 0}\\{y = \frac{3}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = \frac{3}{2}}\end{array}} \right.} \right.\). Vậy \(E\left( {1;\frac{3}{2}} \right)\).
Ta thấy \(T(x;y) = 200x + 100y\) đạt giá trị nhỏ nhất chỉ có thể tại các điểm \(A,B,C,D,E\).
Tại \(A\left( {\frac{3}{8};\frac{3}{2}} \right)\) thì \(T = 200 \cdot \frac{3}{8} + 100 \cdot \frac{3}{2} = 225\) (nghìn đồng).
Tại \(B\left( {\frac{3}{2};0} \right)\) thì \(T = 200 \cdot \frac{3}{2} + 100 \cdot 0 = 300\) (nghìn đồng).
Tại \(C(2;0)\) thì \(T = 200.2 + 100.0 = 400\) (nghìn đồng).
Tại \(D(2;1)\) thì \(T = 200.2 + 100.1 = 500\) (nghìn đồng).
Tại \(E\left( {1;\frac{3}{2}} \right)\) thì \(T = 200.1 + 100 \cdot \frac{3}{2} = 350\) (nghìn đồng).
Như vậy để chi phí bỏ ra thấp nhất mà vẫn đảm bảo nhu cầu dinh dưỡng khi \(x = \frac{3}{8}\) và \(y = \frac{3}{2} \Rightarrow 4{x^2} + {y^2} = 4 \cdot {\left( {\frac{3}{8}} \right)^2} + {\left( {\frac{3}{2}} \right)^2} = \frac{{45}}{{16}}\).
Lời giải
Gọi \(x,y\) (tấn) lần lượt là số tấn nguyên liệu loại \(I\) và loại \(II\) cần sử dụng.
Điều kiện \(0 \le x \le 9;0 \le y \le 7\).
Khi đó số kg chất \(A\) thu được là: \(25x + 20y\)
Số kg chất \(B\) thu được là: \(1,2x + 2y\)
Ta có hệ bất phương trình
\(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 9}\\{0 \le y \le 7}\\{25x + 20y \ge 160}\\{1,2x + 2y \ge 12}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0 \le x \le 9}\\{0 \le y \le 7}\\{5x + 4y \ge 32}\\{3x + 5y \ge 30}\end{array}} \right.} \right.\)
Chi phí mua nguyên liệu là:
\(T(x;y) = 6x + 4y\) (triệu đồng).
Bài toán trở thành tìm giá trị nhỏ nhất của \(T(x;y) = 5x + 4y\) trên miền nghiệm của hệ (*).
Miền nghiệm của hệ bất phương trình là miền được tô màu như hình vẽ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.