Người ta dùng hai loại nguyên liệu để chiết xuất ít nhất \(160\;kg\) hóa chất \(A\) và \(12\;kg\) hóa chất \(B\). Từ mỗi tấn nguyên liệu loại \(I\) giá 5 triệu đồng có thể chiết xuất được \(25\;kg\) chất \(A\) và \(1,2\;kg\) chất \(B\). Từ mỗi tấn nguyên liệu loại \(II\) giá 4 triệu đồng có thể chiết xuất được \(20\;kg\) chất \(A\) và \(2\;kg\) chất \(B\). Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất. Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 9 tấn nguyên liệu loại \(I\) và không quá 7 tấn nguyên liệu loại \(II\).
Người ta dùng hai loại nguyên liệu để chiết xuất ít nhất \(160\;kg\) hóa chất \(A\) và \(12\;kg\) hóa chất \(B\). Từ mỗi tấn nguyên liệu loại \(I\) giá 5 triệu đồng có thể chiết xuất được \(25\;kg\) chất \(A\) và \(1,2\;kg\) chất \(B\). Từ mỗi tấn nguyên liệu loại \(II\) giá 4 triệu đồng có thể chiết xuất được \(20\;kg\) chất \(A\) và \(2\;kg\) chất \(B\). Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất. Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 9 tấn nguyên liệu loại \(I\) và không quá 7 tấn nguyên liệu loại \(II\).
Câu hỏi trong đề: Đề kiểm tra Bài tập cuối chương II (có lời giải) !!
Quảng cáo
Trả lời:
Gọi \(x,y\) (tấn) lần lượt là số tấn nguyên liệu loại \(I\) và loại \(II\) cần sử dụng.
Điều kiện \(0 \le x \le 9;0 \le y \le 7\).
Khi đó số kg chất \(A\) thu được là: \(25x + 20y\)
Số kg chất \(B\) thu được là: \(1,2x + 2y\)
Ta có hệ bất phương trình
\(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 9}\\{0 \le y \le 7}\\{25x + 20y \ge 160}\\{1,2x + 2y \ge 12}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0 \le x \le 9}\\{0 \le y \le 7}\\{5x + 4y \ge 32}\\{3x + 5y \ge 30}\end{array}} \right.} \right.\)
Chi phí mua nguyên liệu là:
\(T(x;y) = 6x + 4y\) (triệu đồng).
Bài toán trở thành tìm giá trị nhỏ nhất của \(T(x;y) = 5x + 4y\) trên miền nghiệm của hệ (*).
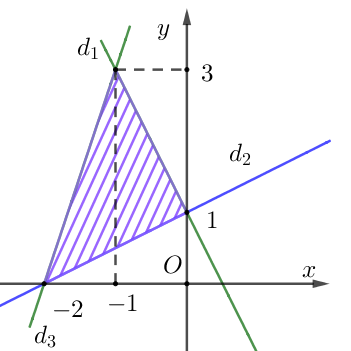
Miền nghiệm của hệ bất phương trình là miền được tô màu như hình vẽ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Điều kiện: \(0 \le x \le 2;0 \le y \le 1,5\)
Khi đó số protein có được là \(800x + 600y\) và số lipit có được là \(200x + 400y\)
Vì gia đình đó cần ít nhất 1200 đơn vị protein và 800 đơn vị lipit trong thức ăn mỗi ngày nên điều kiện tương ứng là:
\(800x + 600y \ge 1200 \Leftrightarrow 4x + 3y \ge 6{\rm{ v\`a }}200x + 400y \ge 800 \Leftrightarrow x + 2y \ge 4\)
Ta có hệ bất phương trình sau:
\(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 2}\\{0 \le y \le 1,5}\\{4x + 3y \ge 6}\\{x + 2y \ge 4}\end{array}} \right.\)(*)
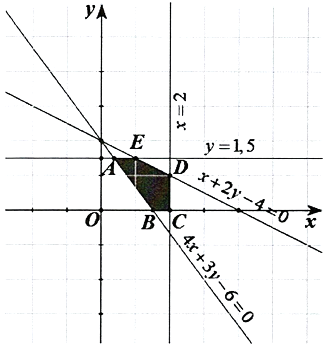
Miền nghiệm của hệ trên là miền ngũ giác \(ABCDE\) kể cả các cạnh của ngũ giác.
Chi phí để mua \(x\;kg\) thịt bò và \(y\;kg\) thịt lợn là \(T = 200x + 100y\) (nghìn đồng).
Bài toán trở thành tìm giá trị nhỏ nhất của \(T(x;y) = 200x + 100y\) trên miền nghiệm của hệ \((*)\).
Tìm tọa độ các điểm \(A,B,C,D,E\).
Tọa độ điểm \(A\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{4x + 5y - 6 = 0}\\{y = \frac{3}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{3}{8}}\\{y = \frac{3}{2}}\end{array}} \right.} \right.\). Vậy \(A\left( {\frac{3}{8};\frac{3}{2}} \right)\).
Tọa độ điềm \(C\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 0}\end{array}} \right.\). Vậy \(C(2;0)\).
Tọa độ điểm \(D\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{x + 2y - 4 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 1}\end{array}} \right.} \right.\). Vậy \(D(2;1)\).
Tọa độ điểm \(E\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x + 2y - 4 = 0}\\{y = \frac{3}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = \frac{3}{2}}\end{array}} \right.} \right.\). Vậy \(E\left( {1;\frac{3}{2}} \right)\).
Ta thấy \(T(x;y) = 200x + 100y\) đạt giá trị nhỏ nhất chỉ có thể tại các điểm \(A,B,C,D,E\).
Tại \(A\left( {\frac{3}{8};\frac{3}{2}} \right)\) thì \(T = 200 \cdot \frac{3}{8} + 100 \cdot \frac{3}{2} = 225\) (nghìn đồng).
Tại \(B\left( {\frac{3}{2};0} \right)\) thì \(T = 200 \cdot \frac{3}{2} + 100 \cdot 0 = 300\) (nghìn đồng).
Tại \(C(2;0)\) thì \(T = 200.2 + 100.0 = 400\) (nghìn đồng).
Tại \(D(2;1)\) thì \(T = 200.2 + 100.1 = 500\) (nghìn đồng).
Tại \(E\left( {1;\frac{3}{2}} \right)\) thì \(T = 200.1 + 100 \cdot \frac{3}{2} = 350\) (nghìn đồng).
Như vậy để chi phí bỏ ra thấp nhất mà vẫn đảm bảo nhu cầu dinh dưỡng khi \(x = \frac{3}{8}\) và \(y = \frac{3}{2} \Rightarrow 4{x^2} + {y^2} = 4 \cdot {\left( {\frac{3}{8}} \right)^2} + {\left( {\frac{3}{2}} \right)^2} = \frac{{45}}{{16}}\).
Lời giải
Gọi \(x,y(ha)\) lần lượt là số \[ha\] trồng bắp và khoai lang.
Điều kiện \(0 \le x \le 4;0 \le y \le 4;x + y \le 4\); \(10x + 15y \le 45 \Rightarrow 2x + 3y \le 9\)
Số tiền thu được là \(T(x,y) = 2x + 2,5y\) (triệu đồng).
Ta có hệ \(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 4}\\{0 \le y \le 4}\\{x + y \le 4}\\{2x + 3y \le 9}\end{array}} \right.\)\((*)\)
Bài toán trở thành tìm giá trị lớn nhất của \(T(x;y) = 2x + 2,5y\) trên miền nghiệm của hệ \((*)\).

Tìm tọa độ các điểm \(O,A,B,C\).
Tọa độ điểm \(A\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x = 0}\\{2x + 3y - 9 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}\\{y = 3}\end{array}} \right.} \right.\). Vậy \(A(0;3)\).
Tọa độ điểm \(B\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x + y - 4 = 0}\\{2x + 3y - 9 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 1}\end{array}} \right.} \right.\). Vậy \(B(3;1)\).
Tọa độ điểm \(C\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x + y - 4 = 0}\\{y = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 4}\\{y = 0}\end{array}} \right.} \right.\). Vậy \(C(4;0)\).
Tọa độ điểm \(O(0;0)\).
Ta thấy \(T(x;y) = 2x + 2,5y\) đạt giá trị lớn nhất chỉ có thể tại các điểm \(O,A,B,C\).
Tại \(A(0;3)\) thì \(T = 2.0 + 2,5.3 = 7,5\) (triệu đồng).
Tại \(B(3;1)\) thì \(T = 2.3 + 2,5.1 = 8,5\) (triệu đồng).
Tại \(C(4;0)\) thì \(T = 2.4 + 2,5.0 = 8\) (triệu đồng).
Tại \(O(0;0)\) thì \(T = 2.0 + 2,5.0 = 0\) (triệu đồng).
Vậy cần trồng \(3ha\) bắp và \(1ha\) khoai lang để thu được số tiền nhiều nhất.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.