Cho tam giác ABC. Khi đó:
a) \(a = b\cos C + c\cos B\)
b) \(\sin A = \sin B\cos C + \sin C\cos B\)
c) \({h_a} = 2R\sin B\sin C\)
d) \({b^2} - {c^2} = a(b\cos C - c\cos B)\)
Cho tam giác ABC. Khi đó:
a) \(a = b\cos C + c\cos B\)
b) \(\sin A = \sin B\cos C + \sin C\cos B\)
c) \({h_a} = 2R\sin B\sin C\)
d) \({b^2} - {c^2} = a(b\cos C - c\cos B)\)
Câu hỏi trong đề: Đề kiểm tra Hệ thức lượng trong tam giác (có lời giải) !!
Quảng cáo
Trả lời:
|
a) Đúng |
b) Đúng |
c) Đúng |
d) Đúng |
a) \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\). \(VP = b\cos C + c\cos B = b \cdot \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} + c \cdot \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\) \( = \frac{{{a^2} + {b^2} - {c^2}}}{{2a}} + \frac{{{a^2} + {c^2} - {b^2}}}{{2a}} = \frac{{2{a^2}}}{{2a}} = a = VP(dpcm)\).
b) \(\sin B = \frac{b}{{2R}};\sin C = \frac{c}{{2R}}\) \(VP = \sin B\cos C + \sin C\cos B = \frac{b}{{2R}} \cdot \cos C + \frac{c}{{2R}} \cdot \cos B = \frac{1}{{2R}}(b\cos C + c\cos B)\)
(mà \(a = b\cos C + c\cos B\), chứng minh câu \(a). = \frac{1}{{2R}} \cdot a = VP(dpcm)\).
c) \(S = \frac{1}{2}a \cdot {h_a} = \frac{1}{2}bc\sin A\) \( \Rightarrow {h_a} = \frac{{bc\sin A}}{a} = \frac{{2R\sin B \cdot 2R\sin C \cdot \sin A}}{{2R\sin A}} = 2R\sin B\sin C = VP(dp\;cm)\).
d) \(a(b\cos C - c\cos B) = ab \cdot \cos C - ac \cdot \cos B = ab \cdot \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} - ac \cdot \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\) \( = \frac{{{a^2} + {b^2} - {c^2}}}{2} - \frac{{{a^2} + {c^2} - {b^2}}}{2} = \frac{{{a^2} + {b^2} - {c^2} - {a^2} - {c^2} + {b^2}}}{2} = {b^2} - {c^2}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
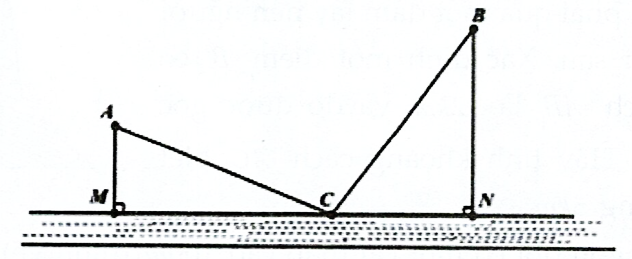
Kẻ \(AK \bot BN;{A^\prime }H \bot BN\).
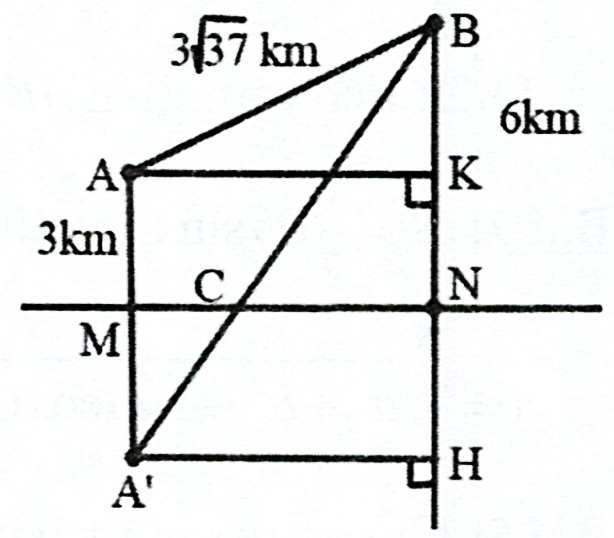
Gọi \({A^\prime }\) đối xứng với \(A\) qua \(MN,D\) là trung của \(NB\).
\(T = CA + CB = C{A^\prime } + CB \ge {A^\prime }B\) (không đổi). Đẳng thức xảy ra khi \(\{ C\} = MN \cap {A^\prime }B\).
\(MN = AK = {A^\prime }H = \sqrt {A{B^2} - K{B^2}} = \sqrt {{{(3\sqrt {37} )}^2} - {3^2}} = 18\;km.\)
Vậy \({A^\prime }B = \sqrt {{A^\prime }{H^2} + H{B^2}} = \sqrt {{{18}^2} + {9^2}} = 9\sqrt 5 \simeq 20,12\;km\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.