Gọi \(S = m_a^2 + m_b^2 + m_c^2\) là tổng bình phương độ dài ba trung tuyến của tam giác \(ABC\). Trong các mệnh đề sau mệnh đề nào đúng?
Câu hỏi trong đề: Đề kiểm tra Bài tập cuối chương III (có lời giải) !!
Quảng cáo
Trả lời:
Chọn A
Ta có: \(S = m_a^2 + m_b^2 + m_c^2 = \frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4} + \frac{{{a^2} + {c^2}}}{2} - \frac{{{b^2}}}{4} + \frac{{{a^2} + {b^2}}}{2} - \frac{{{c^2}}}{4} = \frac{3}{4}({a^2} + {b^2} + {c^2}).\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
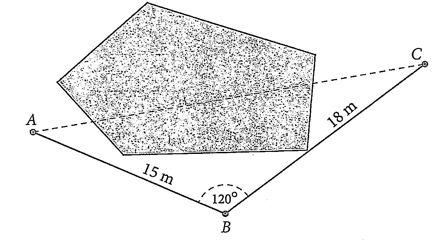
Áp dụng định lí côsin cho tam giác \(ABC\) ta có:
Vậy độ dài dây điện nối từ nhà ra cột điện dài 28,62 m.
Lời giải
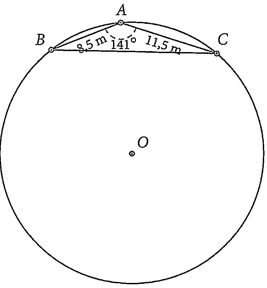
Áp dụng định lí côsin cho tam giác \(ABC\) ta có:
Ta lại có:
Do đó, \(d = 2R \approx 15 \cdot 2 = 30(\;m)\).
Vậy đường kính của hồ nước khoảng \(30\;m\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Cho tam giác \[ABC\] đều cạnh \[2a\]. Tính bán kính \[R\]của đường tròn ngoại tiếp tam giác \[ABC\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.