Bác An cần thiết kế một nhà vườn ngoài trời để trồng hoa. Bác đã thiết kế và vẽ mô hình nhà vườn trong hệ trục toạ độ \[Axyz\] như hình vẽ, với các cột nhà là các đoạn thẳng \[AA',\,BB',\,CC'\] và \[DD'\]. Phần mái là tứ giác \(A'B'C'D'\) và hình vuông \(ABCD\) nằm trên mặt đất. Biết độ dài các đoạn thẳng \(AB = 25\,{\rm{m}},AA' = BB' = 4\,{\rm{m}}\) và \(CC' = DD' = 3\,{\rm{m}}\).
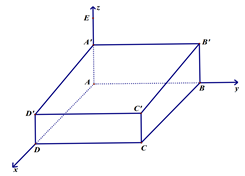
a) Toạ độ điểm \(A'\left( {0;\,0;\,4} \right)\).
b) Đường thẳng \(A'D'\) có phương trình tham số là \[\left\{ {\begin{array}{*{20}{c}}{x = 25t}\\{y = 0\,\,\,\,\,\,}\\{z = 4 - t}\end{array}\,\,\,\begin{array}{*{20}{c}}{}\\{,t \in \mathbb{R}}\\{}\end{array}} \right.\].
c) Bác An đặt một camera ở vị trí \(E\) trên cột \(AA'\) và cách mặt đất \(7\,{\rm{m}}\). Một vật ở vị trí \(M\left( {a;\,b;\,c} \right)\) thoả mãn \(MA = MB = MC = MD = \sqrt {\frac{{697}}{2}} \) thì cách camera \(\frac{{\sqrt {1266} }}{2}{\rm{m}}\).
d) Gọi \(\alpha \) là góc hợp bởi đường thẳng \(A'D'\) và mặt đất. Khi đó \(\cos \alpha = \frac{1}{{\sqrt {626} }}\,\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đúng. Ta có \[AA' = 4\,{\rm{m}}\] nên toạ độ \(A'\left( {0;\,0;\,4} \right)\).
b) Đúng. Toạ độ điểm \(D'\left( {25;\,0;\,3} \right)\) nên vectơ chỉ phương \[{\overrightarrow u _{A'D'}} = \overrightarrow {A'D'} = \left( {25;\,0;\, - 1} \right)\].
Phương trình đường thẳng \(A'D'\) có vectơ chỉ phương \[{\overrightarrow u _{A'D'}} = \left( {25;\,0;\, - 1} \right)\] và đi qua điểm \(A'\left( {0;\,0;\,4} \right)\) là \[\left\{ {\begin{array}{*{20}{c}}{x = 25t}\\{y = 0\,\,\,\,\,\,}\\{z = 4 - t}\end{array}\,\,\,\begin{array}{*{20}{c}}{}\\{,t \in \mathbb{R}}\\{}\end{array}} \right.\].
c) Sai. Điểm \[E\] nằm trên cột \(AA'\) và cách mặt đất 7 m suy ra toạ độ \(E\left( {0;\,0;\,7} \right)\).
Gọi \[I\] là giao điểm của \[AC\]và \[\;BD\]. Do \(ABCD\) là hình vuông có cạnh \(AB = 25\,{\rm{m}}\) nên điểm \[I\]có toạ độ \(I\left( {\frac{{25}}{2};\frac{{25}}{2};0} \right)\) mà \(MA = MB = MC = MD\), do đó \(I\) là hình chiếu của \(M\) lên mặt phẳng \(\left( {ABCD} \right)\). Suy ra \(M\left( {\frac{{25}}{2};\frac{{25}}{2};c} \right)\) mà \(MA = \sqrt {\frac{{697}}{2}} \Leftrightarrow {\left( {\frac{{25}}{2}} \right)^2} + {\left( {\frac{{25}}{2}} \right)^2} + {c^2} = \frac{{697}}{2} \Leftrightarrow c = 6\)
\( \Rightarrow M\left( {\frac{{25}}{2};\frac{{25}}{2};6} \right)\) \( \Rightarrow ME = 17,706\).
d) Sai. Ta có \[\overrightarrow {A'D'} = \left( {25;\,0;\, - 1} \right)\] và vectơ pháp tuyến của mặt đất là \({\overrightarrow n _{\left( {Oxy} \right)}} = \left( {0;\,0;\,1} \right)\) do đó góc hợp với đường thẳng \(A'D'\) và mặt đất là \(\sin \alpha = \frac{{\left| {25.0 + 0.0 + ( - 1).1} \right|}}{{\sqrt {{{25}^2} + {{( - 1)}^2}} .\sqrt {{1^2}} }} = \frac{1}{{\sqrt {626} }}.\)
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(M\left( {a;b;c} \right)\). Khi đó ta có:
\({\left( {a + 1} \right)^2} + {\left( {b - 6} \right)^2} + {\left( {c - 3} \right)^2} = 36 \Leftrightarrow {a^2} + {b^2} + {c^2} + 2a - 12b - 6c + 10 = 0\) \(\left( 1 \right)\)
\({\left( {a - 4} \right)^2} + {\left( {b - 8} \right)^2} + {\left( {c - 1} \right)^2} = 49 \Leftrightarrow {a^2} + {b^2} + {c^2} - 8a - 16b - 2c + 32 = 0\) \(\left( 2 \right)\)
\({\left( {a - 9} \right)^2} + {\left( {b - 6} \right)^2} + {\left( {c - 7} \right)^2} = 144 \Leftrightarrow {a^2} + {b^2} + {c^2} - 18a - 12b - 14c + 22 = 0\) \(\left( 3 \right)\)
\({\left( {a + 15} \right)^2} + {\left( {b - 18} \right)^2} + {\left( {c - 7} \right)^2} = 576 \Leftrightarrow {a^2} + {b^2} + {c^2} + 30a - 36b - 14c + 22 = 0\) \(\left( 4 \right)\)
Giải hệ gồm 4 phương trình trên ta được \(a = 1;b = 2;c = - 1\) nên \(M\left( {1;2; - 1} \right)\).
Vậy \(T = 1 + 2 + \left( { - 1} \right) = 2\).
Đáp án: 2.
Lời giải
Phương trình tham số của đường cáp là: \[d:\left\{ \begin{array}{l}x = - 2\\y = 1 - 2k\\z = 5 + 6k\end{array} \right.\begin{array}{*{20}{c}}{}&{\left( {k \in \mathbb{R}} \right)}\end{array}\]
Do tốc độ chuyển động của cabin là \(4\,{\rm{m/s}}\) nên độ dài \(AM = 4t\) \(\left( m \right)\).
Vì vậy sau \[5\] (s) kể từ lúc xuất phát, cabin đến điểm \[M\] thì \(AM = 4.5 = 20\) \(\left( m \right)\).
Vì \[M \in d \Rightarrow M\left( { - 2;1 - 2k;5 + 6k} \right)\].
\[\overrightarrow {AM} = \left( {0; - 2k;6k} \right)\]. Do 2 vec tơ \[\overrightarrow {AM} ;\vec u\] cùng hướng \(k > 0\).
\(AM = 20 \Leftrightarrow \sqrt {{0^2} + 4{k^2} + 36{k^2}} = 20 \Leftrightarrow 40{k^2} = 400 \Leftrightarrow k = \pm \sqrt {10} \).
Vì \(k > 0 \Rightarrow k = \sqrt {10} \).
Vậy tọa độ \[M\left( { - 2;1 - 2\sqrt {10} ;5 + 6\sqrt {10} } \right)\]. Khi đó \[a + 3b + c = - 2 + 3\left( {1 - 2\sqrt {10} } \right) + 5 + 6\sqrt {10} = 6\].
Đáp án: 6.
Câu 3
A.
\({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 8\).
B.
\({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 2\).
C.
\({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 8\).
D.
\({\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.
\({\left( {x - 1} \right)^2} + {y^2} + {\left( {z + 1} \right)^2} = 9\).
B.
\({\left( {x - 1} \right)^2} + {y^2} + {\left( {z + 1} \right)^2} = 3\).
C.
\({\left( {x + 1} \right)^2} + {y^2} + {\left( {z - 1} \right)^2} = 9\).
D.
\({\left( {x + 1} \right)^2} + {y^2} + {\left( {z - 1} \right)^2} = 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo