Một em nhỏ cân nặng \(m = 25\) kg trượt trên cầu trượt dài 4 m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là 30°.
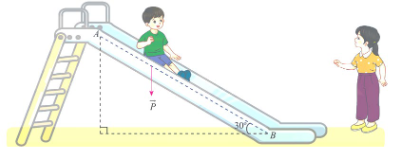
Công \(A\) (N) sinh bởi một lực \(\overrightarrow F \) có độ dịch chuyển \(\overrightarrow d \) được tính bởi công thức \(A = \overrightarrow F .\overrightarrow d \). Hãy tính công sinh bởi trọng lực \(\overrightarrow P = m\overrightarrow g \) khi em nhỏ trượt hết chiều dài cầu trượt, cho biết vectơ gia tốc rơi tự do \(\overrightarrow g \) có độ lớn là \(g = 9,8\) m/s2.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Độ lớn trọng lực tác dụng lên em nhỏ là \(P = m.g = 25.9,8 = 245\) (N).
Công sinh ra bởi trọng lực \(\overrightarrow P \) khi em nhỏ trượt hết chiều dài cầu trượt là
\(A = \overrightarrow P .\overrightarrow d = \left| {\overrightarrow P } \right|.\overrightarrow {\left| d \right|} .\cos \left( {\overrightarrow P ,\overrightarrow d } \right) = 245.4.\cos 60^\circ = 490\) (J).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có 80000 đồng/m2 = 8 đồng/cm2; 100000 đồng/m2 = 10 đồng/cm2.
Gọi \(x\) (cm) là độ dài của một cạnh đáy còn lại của hình hộp, \(h\) (cm) là chiều cao của hình hộp ( \(x > 0,h > 0\)).
Thể tích của khối hộp \(V = x.80.h = 16000 \Rightarrow h = \frac{{16000}}{{80x}} = \frac{{200}}{x}\).
Do đó chi phí làm bể cá là
\(f\left( x \right) = 80x.10 + \left( {2.80.\frac{{200}}{x} + 2x.\frac{{200}}{x}} \right).8 = 800x + \frac{{256000}}{x} + 3200\) đồng.
Yêu cầu bài toán trở thành tìm giá trị nhỏ nhất của hàm số \(f\left( x \right) = 800x + \frac{{256000}}{x} + 3200\) trên \(\left( {0; + \infty } \right)\).
Ta có \(f'\left( x \right) = 800 - \frac{{256000}}{{{x^2}}} = 0 \Leftrightarrow x = 8\sqrt 5 \) vì \(x \in \left( {0; + \infty } \right)\)
Bảng biến thiên
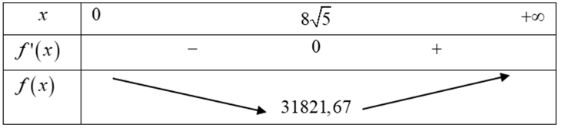
Vậy chi phí ít nhất để làm bể cá như yêu cầu đề bài khoảng 32 nghìn đồng.
Lời giải
a) Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\).
b) Giá trị cực đại của hàm số là 2.
c) \(\mathop {\min }\limits_{\left[ {\frac{1}{2};2} \right]} f\left( x \right) = f\left( 1 \right) = - 2\).
d) Đồ thị hàm số đi qua gốc tọa độ nên \(f\left( 0 \right) = 0 \Rightarrow d = 0\).
Theo đề ta có \(\left\{ \begin{array}{l}f\left( { - 1} \right) = 2\\f\left( 1 \right) = - 2\\f'\left( { - 1} \right) = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l} - a + b - c = 2\\a + b + c = - 2\\3a - 2b + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\\c = - 3\end{array} \right.\).
Suy ra \(f\left( x \right) = {x^3} - 3x\).
Do đó \(f\left( 5 \right) = {5^3} - 3.5 = 110\).
Đáp án: a) Sai; b) Đúng; c) Sai; d) Sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
\(16\).
\(3\).
\(61\).
\(60\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập