Cho biểu thức \(P = \left( {\frac{{2x + 1}}{{\sqrt {{x^3}}  - 1}} - \frac{1}{{\sqrt x  - 1}}} \right):\left( {1 - \frac{{x + 4}}{{x + \sqrt x  + 1}}} \right)\). Các giá trị nguyên của \(x\) để \(P\) nhận giá trị nguyên dương là

Địa y là một dạng kết hợp giữa nấm và một loại sinh vật có thể quang hợp (có thể là tảo lục hay khuẩn lam) trong một mối quan hệ cộng sinh. Địa y tồn tại ở một số môi trường khắc nghiệt nhất thế giới như đài nguyên bắc cực, sa mạc, bờ đá. Chúng rất phong phú trên các lá và cành cây tại rừng mưa và rừng gỗ, trên đá, cả trên tường gạch và đất. Nóc của nhiều tòa nhà cũng có địa y mọc. Địa y rất phổ biến và có thể sống lâu; tuy nhiên, nhiều loại địa y dễ bị tổn thương khi thay đổi thời tiết đột ngột, chúng có thể được các nhà khoa học dùng để đo mức độ ô nhiễm không khí, hay hủy hoại tầng ozone.

Kết quả của sự nóng dần lên của trái đất làm băng tan trên các dòng sông bị đóng băng. Mười hai năm sau khi băng tan, những thực vật nhỏ, được gọi là Địa y, bắt đầu phát triển trên đá. Mỗi nhóm địa y phát triển trên một khoảng đất hình tròn.

Mối quan hệ giữa đường kính \[d,\] tính bằng milimet (mm), của hình tròn và tuổi \[t\] của Địa y có thể biểu diễn tương đối theo công thức:

\(d = 7\sqrt {t - 12} \), với \(t \ge 12\).

An đo đường kính của một số nhóm địa y và thấy có số đo là \[35{\rm{ mm}}.\] Đối với kết quả trên thì băng đã tan cách đó bao nhiêu năm?

Để tính toán thời gian một chu kỳ đong đưa (một chu kỳ đong đưa dây đu được tính từ lúc dây đu bắt đầu được đưa lên cao đến khi dừng hẳn) của một dây đu, người ta sử dụng công thức:

\(T = 2\pi \sqrt {\frac{L}{g}} \).

Trong đó, \[T\] là thời gian một chu kỳ đong đưa (s);

\[L\] là chiều dài của dây đu (m);

\(g = 9,81\;\,{\rm{m}}/{{\rm{s}}^2}.\)

Tốc độ tăng trưởng dân số bình quân hàng năm có thể tính theo công thức:

\(\bar r = \sqrt {\frac{{{P_t}}}{{{P_0}}}}  - 1\).

Trong đó: \({P_0}\): Dân số thời điểm gốc;

\({P_t}\): Dân số thời điểm năm sau;

\[\bar r\]: Tốc độ tăng trưởng dân số bình quân hàng năm.

Tổng số dân Việt Nam năm 2014 là \[90\,\,728,9\] nghìn người. Tổng số dân Việt Nam năm 2015 là \[91\,\,703,8\] nghìn người.

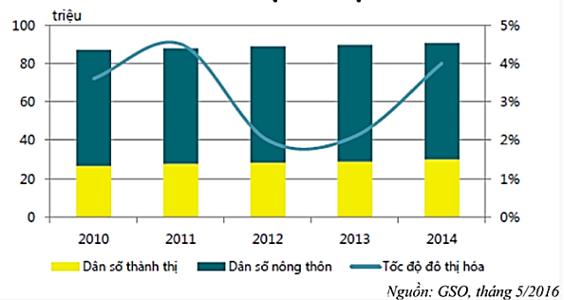Hỏi tốc độ tăng trưởng dân số bình quân hàng năm của Việt Nam trong giai đoạn trên là bao nhiêu phần trăm?

Với \(a > 0\,;\,\,b > 0\), cho biểu thức \(M = \sqrt {\frac{a}{b}}  + \frac{a}{b} \cdot \sqrt {\frac{b}{a}} .\)

a) Kết quả rút gọn biểu thức là \(\sqrt {\frac{{2a}}{b}} \).

b) Giá trị của biểu thức \(M\) với \[a = 1\,;\,\,\,b = 2\] là \[\sqrt 2 \].

c) Biết \[b \cdot M = 1\], khi đó tích \[ab = \frac{1}{2}\].

d) Nếu \[a = b\] thì giá trị biểu thức \[M = 2\].

Vận tốc \(v\,\,({\rm{m}}/{\rm{s}})\) của một tàu lượn di chuyển trên một cung tròn có bán kính \(r\,\,({\rm{m}})\) được cho bởi công thức: \(v = \sqrt {ar} \). Trong đó a là gia tốc của tàu \(\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\) (gia tốc là đại lượng vật lý đặc trưng cho sự thay đổi của vận tốc theo thời gian. Nó là một trong những đại lượng cơ bản dùng để mô tả chuyển động và là độ biến thiên của vận tốc theo thời gian).

Nếu tàu lượn đang chạy với vận tốc \(v = 14\;\,{\rm{m}}/{\rm{s}}\) và muốn đạt mức gia tốc tối đa cho phép là \(a = 9\,\;{\rm{m}}/{{\rm{s}}^2}\) thì bán kính tối thiểu của cung tròn phải là bao nhiêu để xe không văng ra khỏi đường ray?

Vận tốc lăn \(v\) (tính bằng \({\rm{m}}/{\rm{s}}\)) của một vật thể nặng m (tính bằng kg) được tác động một lực \({E_k}\) (gọi là năng lượng Kinetic Energy, ký hiệu \({E_k}\), tính bằng Joule) được cho bởi công thức:

\(v = \sqrt {\frac{{2{E_k}}}{m}} \).

Muốn lăng một quả bowling nặng 3 kg với vận tốc \(6\;{\rm{m}}/{\rm{s}}\), thì cần sử dụng năng lượng Kinetic \({E_k}\) bao nhiêu J?

Cho phương trình \[2\sqrt x  - 6 =  - 2\].

a) Chuyển vế phương trình trên ta được \[2\sqrt x  = 4.\]

b) Nghiệm của phương trình là \[x = 4\].

c) Giá trị của biểu thức \[{x^3}\] với \(x\) là nghiệm của phương trình bằng \[ - 64\].

d) Phương trình đã cho có cùng tập nghiệm với phương trình \[{x^2} - 16 = 0\].