Một người A đứng ở đỉnh của một tòa nhà cao h = 18 m quan sát một chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của người A tới chiếc diều và phương nằm ngang) là \(\alpha = 40^\circ \), khoảng cách từ đỉnh tòa nhà đến mặt người A là 1,6 m. Cùng lúc đó ở dưới chân tòa nhà người B cũng quan sát một chiếc diều, nhận thấy góc nâng là \(\beta = 80^\circ \), khoảng cách từ mặt đất đến mắt người B là 1,5 m. Hỏi chiếc diều bay cao so với mặt đất bao nhiêu mét?
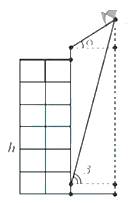
Một người A đứng ở đỉnh của một tòa nhà cao h = 18 m quan sát một chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của người A tới chiếc diều và phương nằm ngang) là \(\alpha = 40^\circ \), khoảng cách từ đỉnh tòa nhà đến mặt người A là 1,6 m. Cùng lúc đó ở dưới chân tòa nhà người B cũng quan sát một chiếc diều, nhận thấy góc nâng là \(\beta = 80^\circ \), khoảng cách từ mặt đất đến mắt người B là 1,5 m. Hỏi chiếc diều bay cao so với mặt đất bao nhiêu mét?

Quảng cáo
Trả lời:
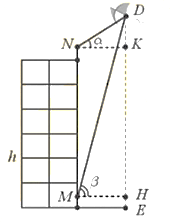
Đặt tên các điểm như hình vẽ.
Xét tam giác MDN có MN = 18 + 1,6 – 1,5 = 18,1 m.
Ta có \(\widehat {MND} = 90^\circ + 40^\circ = 130^\circ \); \(\widehat {NMD} = 90^\circ - 80^\circ = 10^\circ \); \(\widehat {NDM} = 180^\circ - 130^\circ - 10^\circ = 40^\circ \).
Áp dụng định lí sin trong tam giác \(MDN\) ta có \(\frac{{MN}}{{\sin D}} = \frac{{MD}}{{\sin N}} \Rightarrow MD = \frac{{MN}}{{\sin D}}\sin N = \frac{{18,1}}{{\sin 40^\circ }}.\sin 130^\circ \).
Xét DMDH vuông tại H có \(DH = DM.\sin \beta = \frac{{18,1}}{{\sin 40^\circ }}.\sin 130^\circ .\sin 80^\circ \approx 21,2\) m.
Do đó DE = DH + HE = 21,2 + 1,5 = 22,7 m.
Vậy chiếc diều cách mặt đất khoảng 22,7 m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
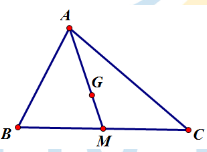
Do M là trung điểm của BC nên ta có \(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GM} \). Chọn A.
Câu 2
Lời giải
Điều kiện: \(x - 1 > 0 \Leftrightarrow x > 1\).
Vậy tập xác định của hàm số là \(D = \left( {1; + \infty } \right)\). Chọn C.
Câu 3
Cho hình chữ nhật \(ABCD\) tâm O có \(AB = 4;BC = 3\).
a) \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng.
b) \(\left| {\overrightarrow {AB} + \overrightarrow {BC} } \right| = 7\).
c) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \), với M là điểm bất kì.
d) \(\overrightarrow {AB} .\overrightarrow {AC} = 16\).
Cho hình chữ nhật \(ABCD\) tâm O có \(AB = 4;BC = 3\).
a) \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng.
b) \(\left| {\overrightarrow {AB} + \overrightarrow {BC} } \right| = 7\).
c) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \), với M là điểm bất kì.
d) \(\overrightarrow {AB} .\overrightarrow {AC} = 16\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.