Phần 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hình vẽ, biết tam giác \(ABC\) vuông tại \(A\) có \(AB = 3AC.\) Trên \(AB\) lấy các điểm \(D,\,\,E\) sao cho \(AD = DE = EB.\)

a) \[\widehat {ACD} = 30^\circ .\]
b) \(CD = AC\sqrt 2 \,\,{\rm{cm}}.\)
c) \(\widehat {AEC} > 30^\circ .\)
d) \(\tan \widehat {AEC} + \tan \widehat {ABC} = \frac{5}{6}.\)
Phần 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hình vẽ, biết tam giác \(ABC\) vuông tại \(A\) có \(AB = 3AC.\) Trên \(AB\) lấy các điểm \(D,\,\,E\) sao cho \(AD = DE = EB.\)

a) \[\widehat {ACD} = 30^\circ .\]
b) \(CD = AC\sqrt 2 \,\,{\rm{cm}}.\)
c) \(\widehat {AEC} > 30^\circ .\)
d) \(\tan \widehat {AEC} + \tan \widehat {ABC} = \frac{5}{6}.\)
Câu hỏi trong đề: Đề kiểm tra Toán 9 Kết nối tri thức Chương 4 có đáp án !!
Quảng cáo
Trả lời:
a) Sai. Vì tam giác \(ABC\) vuông tại \(A\) nên \[\widehat {ACD} = 45^\circ .\]
b) Đúng. Xét tam giác \(ACD\) vuông tại \(A\), ta có: \(CD = \frac{{AC}}{{\sin 45^\circ }} = \frac{{AC}}{{\frac{{\sqrt 2 }}{2}}} = AC\sqrt 2 \,\,{\rm{(cm)}}.\)
c) Sai. Ta có: \(\tan \widehat {AEC} = \frac{1}{2}\) nên \(\widehat {AEC} \approx 27^\circ < 30^\circ .\)
d) Đúng. Ta có: \(\tan \widehat {AEC} + \tan \widehat {ABC} = \frac{1}{2} + \frac{1}{3} = \frac{5}{6}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
![núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\] Đáp án: 1906. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/10/63-1761201081.png)
Gọi \[D\] và \[E\] lần lượt là điểm đặt mắt khi người quan sát đỉnh núi đứng ở vị trí \[B\] và \[C.\]
Gọi \[I\] là hình chiếu của điểm \[D\] trên \[AH\].
So với mặt đất thì \[BD\] và \[CE\] là phương thẳng đứng; \[HC\] và \[IE\] là phương ngang nên các tứ giác \[IHBD,\,\,IHCE,\,\,DBCE\] là hình chữ nhật.
Do đó \[DE = BC = \,475\,\,{\rm{m}}\]; \[IH = DB = EC = 1,6\,\,{\rm{m}}\].
• Xét \[\Delta AID\] vuông tại \[I\] nên:
\[ID = AI \cdot \,\cot \widehat {ADI} = AI \cdot \,\cot 34^\circ = AI \cdot \tan 56^\circ \] (do \[\cot 34^\circ = \tan 56^\circ \]). \[\left( 1 \right)\]
• Xét \[\Delta AIE\] vuông tại \[I\] nên:
\[IE = AI \cdot \,\cot \widehat {AEI} = AI \cdot \,\cot 30^\circ = AI \cdot \tan 60^\circ \] (do \[\cot 30^\circ = \tan 60^\circ \]). \[\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[IE - ID = AI\left( {\tan 60^\circ - \tan 56^\circ } \right)\]
\[AI\left( {\tan 60^\circ - \tan 56^\circ } \right) = 475\]
\[AI = \frac{{475}}{{\tan 60^\circ - \tan 56^\circ }} \approx 1\,\,903,9\,\,({\rm{m}}).\]
Chiều cao \[AH\] của ngọn núi là:
\[AH = AI + IH \approx 1903,9\, + 1,6\, \approx 1906\,\,({\rm{m)}}{\rm{.}}\]
Vậy chiều cao \[AH\] của ngọn núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\]
Đáp án: 1906.
Câu 2
Lời giải
Chọn B
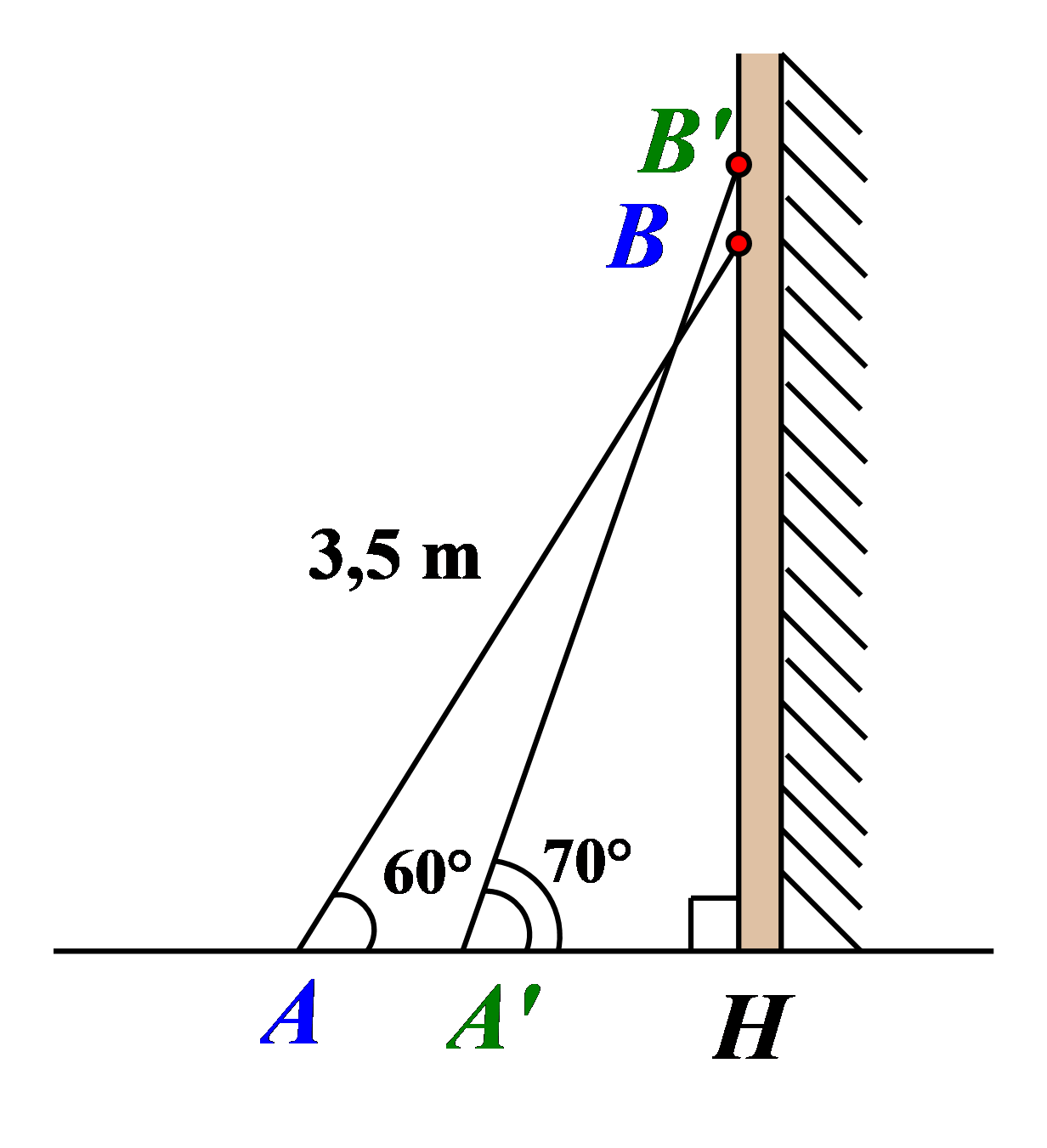
Gắn dữ kiện của bài toán vào mô hình Toán học như trên hình vẽ.
Khi thang tạo với mặt đất một góc có độ lớn \[6{\rm{0}}^\circ \] và \[7{\rm{0}}^\circ \] thì khoảng cách từ chân thang đến chân tường lần lượt là \[AH\] và \[A'H'\].
• Tam giác \[ABH\] vuông tại \[H\] có \[AH = AB \cdot \cos A = 3,5\cos 60^\circ = 1,75\,\,({\rm{m}})\].
• Tam giác \[A'B'H\] vuông tại \[H\] có \[A'H = A'B' \cdot \cos A' = 3,5\cos 70^\circ \approx 1,20\,\,({\rm{m}})\].
Do đó \[1,20\, \le x \le 1,75\].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![núi là \[1\,\,906\,\,{\rm{m}}{\rm{.}}\] Đáp án: 1906. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/62-1761201093.png)
![Hỏi tòa nhà đó cao bao nhiêu tầng, biết rằng mỗi tầng cao \[2\,\,{\rm{m}}?\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/57-1761200288.png)