B. TỰ LUẬN
Tìm các khoảng đơn điệu và cực trị của các hàm số sau:
a) \(f(x) = - {x^3} + 3{x^2}\); b)\(g(x) = x + \frac{1}{x}\); c) \(h(x) = {x^3}\).
B. TỰ LUẬN
Tìm các khoảng đơn điệu và cực trị của các hàm số sau:
a) \(f(x) = - {x^3} + 3{x^2}\); b)\(g(x) = x + \frac{1}{x}\); c) \(h(x) = {x^3}\).
Quảng cáo
Trả lời:
a) Xét hàm số \(f(x) = - {x^3} + 3{x^2}\).
Tập xác định: \(D = \mathbb{R}\).
Ta có \(f'(x) = - 3{x^2} + 6x;f'(x) = 0 \Leftrightarrow x = 0\) hoặc \(x = 2\).
Bảng biến thiên:
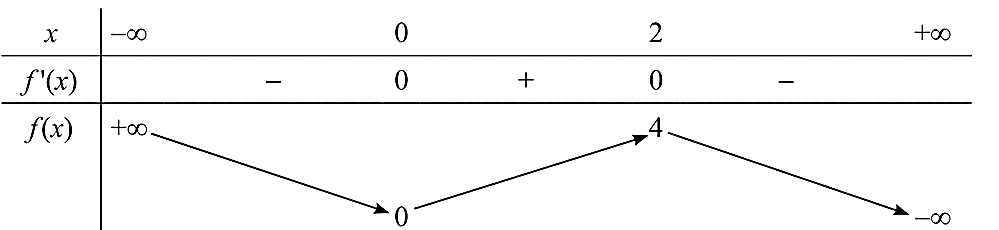
Vậy hàm số \(f(x) = - {x^3} + 3{x^2}\) đồng biến trên khoảng \((0;2)\), nghịch biến trên các khoảng \(( - \infty ;0)\) và \((2; + \infty )\).
Hàm số đạt cực tiểu tại \(x = 0\) và \({y_{CT}} = 0\).
Hàm số đạt cực đại tại \(x = 2\) và .
b) Xét hàm số \(g(x) = x + \frac{1}{x}\).
Tập xác định: \(D = \mathbb{R}\backslash \{ 0\} \).
Ta có \(g'(x) = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}}\).
Vì \({x^2} > 0\) với mọi \(x \in \mathbb{R}\backslash \{ 0\} \) nên \(g'(x)\) cùng dấu với \({x^2} - 1\).
Ta có \(g'(x) = 0 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow x = - 1\) hoặc \(x = 1\).
Bảng biến thiên:
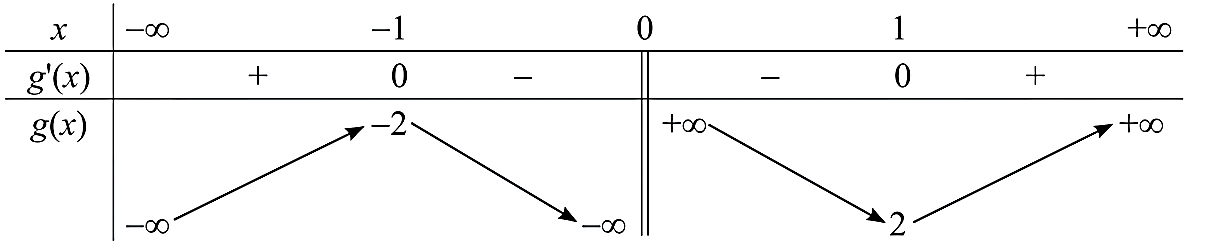
Vậy hàm số \(g(x) = x + \frac{1}{x}\) đồng biến trên các khoảng \(( - \infty ; - 1)\) và \((1; + \infty )\), nghịch biến trên các khoảng \(( - 1;0)\) và \((0;1)\).
Hàm số đạt cực đại tại \(x = - 1\) và .
Hàm số đạt cực tiểu tại \(x = 1\) và \({y_{CT}} = 2\).
c) Xét hàm số \(h(x) = {x^3}\).
Tập xác định: \(D = \mathbb{R}\).
Ta có \(h'(x) = 3{x^2};h'(x) = 0 \Leftrightarrow x = 0\).
Bảng biến thiên:
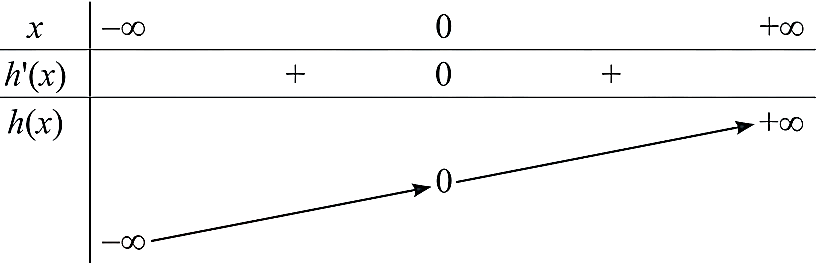
Vậy hàm số \(h(x) = {x^3}\) đồng biến trên \(\mathbb{R}\) và không có cực trị.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có bảng sau:
|
Nhóm |
Giá trị đại diện |
Tần số |
|
\(\left[ {30;40} \right)\) |
35 |
5 |
|
\(\left[ {40;50} \right)\) |
45 |
8 |
|
\(\left[ {50;60} \right)\) |
55 |
25 |
|
\(\left[ {60;70} \right)\) |
65 |
20 |
|
\(\left[ {70;80} \right)\) |
75 |
2 |
|
|
|
\(n = 60\) |
a) Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{35.5 + 45.8 + 55.25 + 65.20 + 75.2}}{{60}} = 56\)(nghìn đồng).
b) Khoảng biến thiên của mẫu số liệu trên là: \(80 - 30 = 50\)(nghìn đồng).
c) Nhóm chứa tứ phân vị thứ nhất là \(\left[ {50;60} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = 50 + \frac{{\frac{{60}}{4} - 13}}{{25}}.10 = 50,8\)(nghìn đồng).
Nhóm chứa tứ phân vị thứ ba là \(\left[ {60;70} \right)\).
Tứ phân vị thứ ba của mẫu số liệu là: \({Q_3} = 60 + \frac{{\frac{{3.60}}{4} - 38}}{{20}}.10 = 63,5\)(nghìn đồng).
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 63,5 - 50,8 = 12,7\)(nghìn đồng).
d) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{5{{\left( {35 - 56} \right)}^2} + 8{{\left( {45 - 56} \right)}^2} + 25{{\left( {55 - 56} \right)}^2} + 20{{\left( {65 - 56} \right)}^2} + 2{{\left( {75 - 56} \right)}^2}}}{{60}} = \frac{{277}}{3} \approx 92,3\)(nghìn đồng).
Đáp án: a) Đúng; b) Đúng; c) Đúng; c) Sai.
Lời giải
Ta có \(y' = 6{x^2} - 6x - 6m\).
Hàm số nghịch biến trên khoảng \(\left( { - 1;\,1} \right)\) khi và chỉ khi \(y' \le 0\) với \(\forall x \in \left( { - 1;\,1} \right)\) hay \(m \ge {x^2} - x\) với \(\forall x \in \left( { - 1;\,1} \right)\).
Xét \(f\left( x \right) = {x^2} - x\) trên khoảng \(\left( { - 1;\,1} \right)\) ta có \(f'\left( x \right) = 2x - 1\); \(f'\left( x \right) = 0 \Leftrightarrow x = \frac{1}{2}\).
Bảng biến thiên
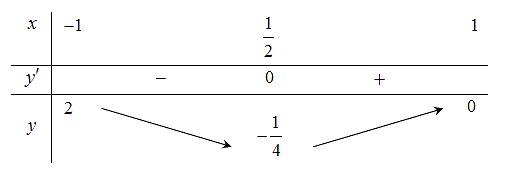
Dựa vào bảng biến thiên ta có \(m \ge f\left( x \right)\)với \[\forall x \in \left( { - 1;\,1} \right)\]\( \Leftrightarrow m \ge 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(s = 161,4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Đo chiều cao (tính bằng \[{\rm{cm}}\]) của \[500\] học sinh trong một trường THPT ta thu được kết quả như sau: Độ lệch chuẩn của mẫu số liệu trên là: A. \(s = 161,4\). B. \(s = 14,48\). C. \(s = 8,2\). D. \(s = 3,85\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/10-1761395174.png)