Cho hàm số \(y = \frac{{ - m{x^2} + (4\;m - 2)x + 1 - 4\;m}}{{x - 1}}\)
a) Khi \[m < - 1\] thì hàm số đạt cực đại và cực tiểu trong miền \(x > 0\)
b) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị
c) Có 2 phương trình tiếp tuyến của \((C)\) song song với đường thẳng \(x - y = 0\)
d) Khi \(m = 1\) đồ thị hàm số không cắt trục \(Ox\)
Cho hàm số \(y = \frac{{ - m{x^2} + (4\;m - 2)x + 1 - 4\;m}}{{x - 1}}\)
a) Khi \[m < - 1\] thì hàm số đạt cực đại và cực tiểu trong miền \(x > 0\)
b) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị
c) Có 2 phương trình tiếp tuyến của \((C)\) song song với đường thẳng \(x - y = 0\)
d) Khi \(m = 1\) đồ thị hàm số không cắt trục \(Ox\)
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
|
a) |
Đ |
b) |
Đ |
c) |
Đ |
d) |
Đ |
Khi \(m = 1:y = \frac{{ - {x^2} + 2x - 3}}{{x - 1}} = - x + 1 - \frac{2}{{x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 1\} \)
\({y^\prime } = \frac{{ - {x^2} + 2x + 1}}{{{{(x - 1)}^2}}} = 0 \Leftrightarrow - {x^2} + 2x + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1 - \sqrt 2 \Rightarrow y = 2\sqrt 2 }\\{x = 1 + \sqrt 2 \Rightarrow y = - 2\sqrt 2 }\end{array}} \right.\)
\(\mathop {\lim }\limits_{x \to 1 \pm } y = \pm \infty :x = 1\)là tiệm cận đứng
\(\mathop {\lim }\limits_{x \to \pm x} y = - x + 1:y = - x + 1\)là tiệm cận xiên
Bảng biến thiên:
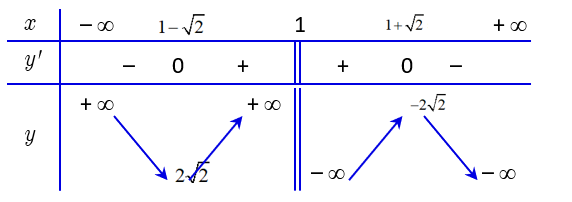
\(x = 0 \Rightarrow y = 3\)
\(y = 0 \Rightarrow - {x^2} + 2x - 3 = 0\), đồ thị hàm số không cắt trục \(Ox\)
\(y = \frac{{ - m{x^2} + (4m - 2)x + 1 - 4m}}{{x - 1}} \Rightarrow {y^\prime } = \frac{{ - m{x^2} + 2mx - 4m + 2 - 1 + 4m}}{{{{(x - 1)}^2}}}\)
Suy ra \({y^\prime } = \frac{{ - m{x^2} + 2mx + 1}}{{{{(x - 1)}^2}}}\)
Dấu \({y^\prime }\) là dấu của tam thức \(g(x) = - m{x^2} + 2mx + 1\)
\(\begin{array}{l}g(x){\rm{ c\'o }}{\Delta ^\prime } = {m^2} + m\\g(1) = - m + 2m + 1 = m + 1\end{array}\)
Để hàm số có cực đại và cực tiểu thì \(\left\{ {\begin{array}{*{20}{l}}{{\Delta ^\prime } > 0}\\{m + 1 \ne 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m < - 1}\\{m > 0}\end{array}} \right.} \right.\)
Lúc này, hàm số đạt cực đại, cực tiểu tại \(x = {x_1},x = {x_2}\) và \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2}\\{{x_1} \cdot {x_2} = - \frac{1}{m}}\end{array}} \right.\).
Giả sử \({x_1} < {x_2}\)
Theo yêu cầu bài toán:
\(\left\{ {\begin{array}{*{20}{l}}{{x_1} > 0}\\{{x_2} > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} > 0}\\{{x_1} \cdot {x_2} > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2 > 0{\rm{ (lu\^o n d\'u ng) }}}\\{ - \frac{1}{m} > 0}\end{array} \Leftrightarrow m < 0} \right.} \right.} \right.\)
Giao với điều kiện \({\Delta ^\prime } > 0\) được \(m < - 1\)
\(y_x^\prime = \frac{{ - {x^2} + 2x + 1}}{{{{(x - 1)}^2}}}\)
Đường thẳng \(x - y = 0\) có hệ số góc \(k = 1\)
Để tiếp tuyến của \((C)\) song song với đường thẳng \(y = x\), cần và đủ là
\(\begin{array}{*{20}{l}}{y_x^\prime = 1}&{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 1}\\{\frac{{ - {x^2} + 2x + 1}}{{{{(x - 1)}^2}}} = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 1}\\{ - {x^2} + 2x + 1 = {x^2} - 2x + 1}\end{array}} \right.} \right.}\\{}&{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 1}\\{2{x^2} - 4x = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0 \Rightarrow y = 3}\\{x = 2 \Rightarrow y = - 3}\end{array}} \right.} \right.}\end{array}\)
Có hai tiếp tuyến thỏa yêu cầu bài toán:
\(\begin{array}{l}\left( {{T_1}} \right):y = 1(x - 0) + 3 \Leftrightarrow y = x + 3\\\left( {{T_2}} \right):y = 1(x - 2) - 3 \Leftrightarrow y = x - 5\end{array}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
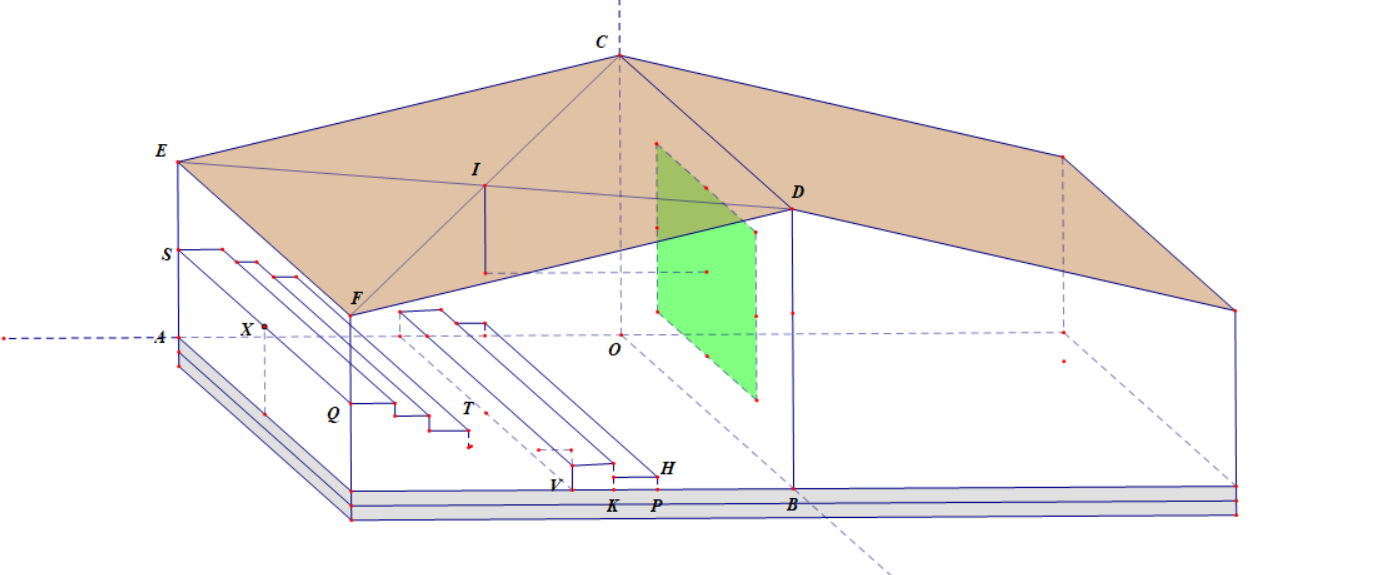
Xét hệ toạ độ \(Oxyz\) với \(O\) là gốc toạ độ, các điểm \(A \in Ox,B \in Oy,C \in Oz\) có toạ độ không âm.
Khi đó \(A(30;0;0),B(0;20;0),D(0;20;10);E(30;0;6)\), \(I(15;10;8)\) là trung điểm \(DE\) nên hình chiếu của điểm \(I\) trên sàn là \(T(15;10;0)\) suy ra toạ độ điểm \(V(15;20;0)\), vậy \(V\) cách \(P\) một khoảng bằng 5 m. Tức là bậc thang tại vị trí \(U\) đang là bậc thang thứ 3, có chiều cao 60 cm so với mặt sàn. Vậy toạ độ điểm \(U(15;10;0,6)\).
Từ đó toạ độ đỉnh đầu học sinh đứng là \(K(15;10;2,4)\). Khoảng cách \(IK = 8 - 2,4 = 5,6m\).
Mặt khác toạ độ điểm \(X(15;10;2)\) nên toạ độ mắt học sinh ngồi tại \(X\) là điểm \(Z(15;10;3,2)\) suy ra hiệu khoảng cách từ điểm \(I\) đến sàn và từ điểm \(Z\) đến sàn nhà là \(8 - 3,2 = 4,8m\)
Điều và cho thấy tổng độ dài của thanh treo và thân máy chiếu không quá 4,8 mét để thoả mãn đồng thời cả 2 điều kiện.
Lời giải
Gọi chiều dài, chiều rộng lần lượt của khung cửa sổ là \(x,y\) . Điều kiện \(x,y > 0\).
Diện tích của khung cửa sổ là \(xy = 3,4 \Rightarrow y = \frac{{3,4}}{x}\).
Khi đó chu vi của khung cửa sổ là \(C = 2x + 2y = 2x + \frac{{6,8}}{x}\).
Xét hàm số \(f(x) = 2x + \frac{{6,8}}{x}\) trên \((0; + \infty )\).
Ta có \(f\prime (x) = 2 - \frac{{6,8}}{{{x^2}}}\)
Cho \(f\prime (x) = 0 \Rightarrow x = \frac{{\sqrt {85} }}{5} \in (0; + \infty )\)
Ta có bảng biến thiên như sau
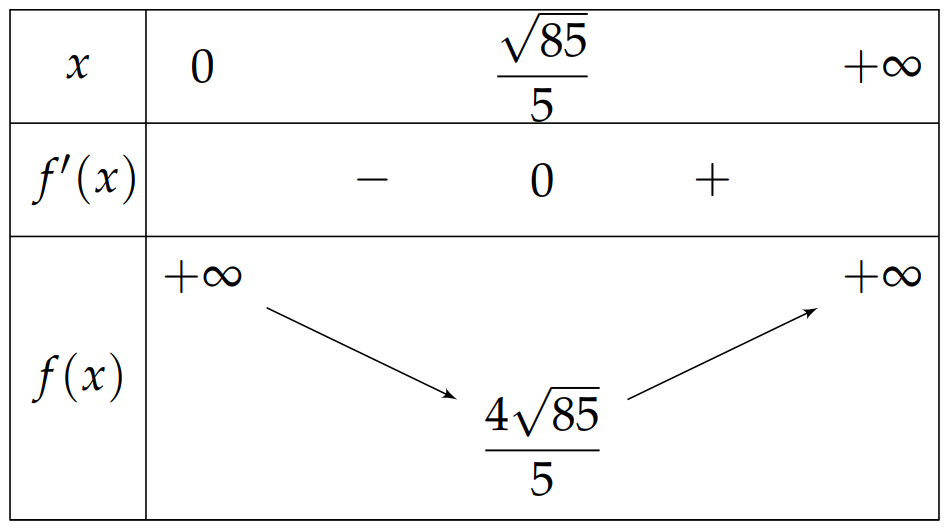
Dựa vào bảng biến thiên ta thấy được chu vi khung cửa sổ nhỏ nhất bằng \(\frac{{4\sqrt {85} }}{5} \approx 7,34\) m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.