PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
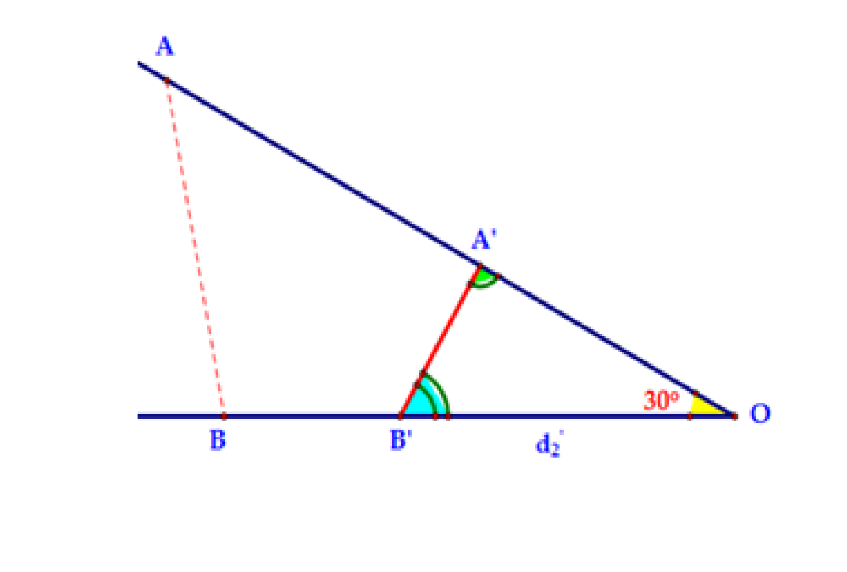
Hai chất điểm \(A\) và \(B\) chuyển động thẳng đều cùng hướng về \(O\) (như hình vẽ), biết rằng vận tốc \({V_B} = \frac{{{V_A}}}{{\sqrt 3 }}\) và góc . Biết rằng khi khoảng cách giữa hai chất điểm \(A\) và \(B\) là nhỏ nhất thì số đo góc \(\widehat {BAO} = \gamma .\) Tìm \(\gamma .\)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Hai chất điểm \(A\) và \(B\) chuyển động thẳng đều cùng hướng về \(O\) (như hình vẽ), biết rằng vận tốc \({V_B} = \frac{{{V_A}}}{{\sqrt 3 }}\) và góc . Biết rằng khi khoảng cách giữa hai chất điểm \(A\) và \(B\) là nhỏ nhất thì số đo góc \(\widehat {BAO} = \gamma .\) Tìm \(\gamma .\)Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \({d_1},{d_2}\) lần lượt là khoảng cách các vật \(A\) và \(B\) đến \(O\) lúc đầu (\(t = 0\)), đồng thời \[d = AB\]. Gọi \(t'\)là thời điểm mà \({d_{\min }}\). Khi đó \(A\) ở \(A'\) và \(B\) ở \(B'\) như hình vẽ.
Kí hiệu góc .
Áp dụng định lý sin trong tam giác \(\Delta A'B'O\) ta có:
\(\frac{d}{{{\mathop{\rm s}\nolimits} {\rm{in}}\,30}} = \frac{{OA'}}{{\sin \gamma }} = \frac{{OB'}}{{\sin \beta }} \Leftrightarrow 2d = \frac{{{d_1} - AA'}}{{\sin \gamma }} = \frac{{{d_2} - BB'}}{{\sin \beta }} \Leftrightarrow 2d = \frac{{{d_1} - {v_1}t}}{{\sin \gamma }} = \frac{{{d_2} - {v_2}t}}{{\sin \beta }}\left( * \right)\)
Do \({v_2} = \frac{{{v_1}}}{{\sqrt 3 }}\) và áp dụng \(\frac{A}{B} = \frac{C}{D} = \frac{{C - A}}{{D - B}}\), ta có:
\(\left( * \right) \Leftrightarrow 2d = \frac{{\sqrt 3 {d_2} - {d_1}}}{{\sqrt 3 \sin \beta - \sin \gamma }}\)mà \(\sin \beta = \sin \left( {{{180}^0} - \beta } \right) = \sin \left( {{{30}^0} + \gamma } \right)\)
Do đó ta có \(d = \frac{{\sqrt 3 {d_2} - {d_1}}}{{2\left[ {\sqrt 3 \sin \left( {{{30}^0} + \gamma } \right) - \sin \gamma } \right]}} = \frac{{\sqrt 3 {d_2} - {d_1}}}{{\sqrt 3 \cos \gamma + \sin \gamma }}\)
Xét \(f\left( \gamma \right) = \sqrt 3 \cos \gamma + \sin \gamma \). Ta có \({d_{\min }} \Leftrightarrow f{\left( \gamma \right)_{\max }}\)
\(f'\left( \gamma \right) = - \sqrt 3 \sin \gamma + c{\rm{os}}\gamma ;f'\left( \gamma \right) = 0 \Leftrightarrow - \sqrt 3 \sin \gamma + c{\rm{os}}\gamma = 0 \Leftrightarrow \tan \gamma = \frac{1}{{\sqrt 3 }} \Leftrightarrow \gamma = {30^0}.\)
\(f''\left( \gamma \right) = - \sqrt 3 {\rm{cos}}\gamma - {\rm{sin}}\gamma ;f''\left( {{{30}^0}} \right) = - \sqrt 3 {\rm{cos}}{30^0} - {\rm{sin}}{30^0} = - 2 < 0\)
Vậy, khi \(\gamma = {30^0}\) thì khoảng cách giữa hai chất điểm \(A\) và \(B\) là nhỏ nhất.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
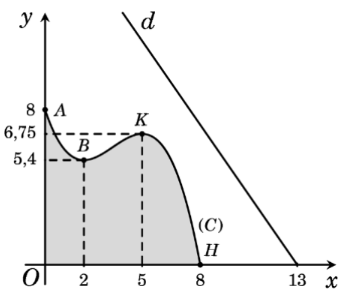
Đồ thị \(\left( C \right)\) của một hàm số bậc ba có dạng: \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\;\left( {a \ne 0} \right)\).
Vì đồ thị \(\left( C \right)\) đi qua các điểm \(A\left( {0;8} \right),B\left( {2;5,4} \right),K\left( {5;6,75} \right)\) và \(H\left( {8;0} \right)\) nên ta có:
\(\left\{ \begin{array}{l}d = 8\\8a + 4b + 2c + d = 5,4\\125a + 25b + 5c + d = 6,75\\512a + 64b + 8c + d = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{{10}}\\b = \frac{{21}}{{20}}\\c = - 3\\d = 8\end{array} \right.\).
Suy ra \(f\left( x \right) = - \frac{1}{{10}}{x^3} + \frac{{21}}{{20}}{x^2} - 3x + 8\).
Điểm \(M\) thuộc \(\left( C \right)\) sao cho khoảng cách từ \(M\) đến \(d\) là nhỏ nhất khi và chỉ khi tiếp tuyến của \(\left( C \right)\) tại \(M\) song song với \(d\) (\(\left( {{x_M} > 5} \right)\).
Ta có: \(f'\left( x \right) = - \frac{3}{{10}}{x^2} + \frac{{21}}{{10}}x - 3\).
Đường thẳng \(d\) có hệ số góc \(k = - \frac{{13}}{9}\).
Suy ra: \( - \frac{3}{{10}}{x^2} + \frac{{21}}{{10}}x - 3 = - \frac{{13}}{9} \Leftrightarrow \left[ \begin{array}{l}x = 6,16\\x = 0,84 < 5\end{array} \right.\).
Do \({x_M} > 5\) nên \({x_M} = 6,16\) thỏa mãn.
Lời giải
Gọi \(x{\rm{ }}\left( {x > 0} \right)\,\,\)nghìn là số tiền giá vé giảm.
Khi đó giá vé sau khi giảm là \(100 - x\,\) (nghìn đồng).
Sau mỗi lần giảm giá thì có thêm 300x khán giả.
Do đó tổng số khán giả đến xem là 27000 + 300x.
Vì sân vận động có sức chứa 55 000 khán giá nên \(27000 + 300x \le 55000 \Leftrightarrow x \le \frac{{280}}{3}\,\)
Doanh thu từ tiền bán vé là:\(y = \left( {27000 + 300x} \right)\left( {100 - x} \right) = - 300{x^2} + 3000x + 2700000\,\)
Yêu cầu bài toán trở thành tìm giá trị lớn nhất của hàm số \(y = - 300{x^2} + 3000x + 2700000{\rm{ }}\,\)
Tập xác định \[{\rm{D}} = \left( {0;\frac{{280}}{3}} \right]\,\]
\(y' = - 600x + 3000.{\rm{ }}y' = 0 \Leftrightarrow x = 5\)
Bảng biến thiên:
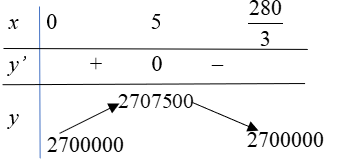
Dựa vào bảng biến thiên, ta thấy ban tổ chức nên đặt giá vé là 95 nghìn đồng thì doanh thu tiền bán vé là lớn nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo