Cho hình lập phương\(ABCD.A'B'C'D'\) cạnh \(a\). Khẳng định nào sau đây là sai?
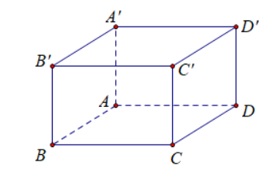
Cho hình lập phương\(ABCD.A'B'C'D'\) cạnh \(a\). Khẳng định nào sau đây là sai?

A. \[\left| {\overrightarrow {BD} } \right| = a\sqrt 2 \].
B. \[\left| {\overrightarrow {BD'} } \right| = a\sqrt 3 \].
C. \[\overrightarrow {AC} + \overrightarrow {A'C'} = \vec 0\].
D. \[\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \].
Quảng cáo
Trả lời:
Ta có \[\left| {\overrightarrow {BD} } \right| = BD = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \] nên khẳng định ở phương án A đúng.
\[\left| {\overrightarrow {BD'} } \right| = BD' = \sqrt {{a^2} + {a^2} + {a^2}} = a\sqrt 3 \] nên khẳng định ở phương án B đúng.
Theo quy tắc hình hộp, ta có \[\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \] nên khẳng định ở phương án D đúng.
Ta có \(\overrightarrow {AC} + \overrightarrow {A'C'} = \overrightarrow {AC} + \overrightarrow {AC} = 2\overrightarrow {AC} \ne \overrightarrow 0 \) nên khẳng định ở phương án C sai. Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
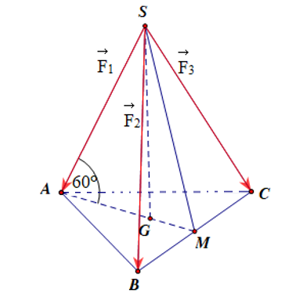
Gán các lực \[\overrightarrow {{F_1}} = \overrightarrow {SA} ,\,\,\overrightarrow {{F_2}} = \overrightarrow {SB} ,\,\,\overrightarrow {{F_3}} = \overrightarrow {SC} .\]
Vì \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|\) và góc tạo bởi mỗi chân của giá đỡ với mặt đất bằng \(60^\circ \) nên \(S.ABC\) là hình chóp đều.
Gọi \(M\) là trung điểm \(BC,\,\,G\) là trọng tâm \(\Delta ABC \Rightarrow SG \bot \left( {ABC} \right).\)
Ta có \(\widehat {SAG} = 60^\circ \Rightarrow SG = SA \cdot \sin 60^\circ = \frac{{SA\sqrt 3 }}{2} \Rightarrow SA = \frac{{2SG}}{{\sqrt 3 }}.\)
Đặt \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \Rightarrow \left| {\overrightarrow F } \right| = 30\left( {\rm{N}} \right){\rm{.}}\)
Vì \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \Rightarrow \left| {\overrightarrow F } \right| = 3\left| {\overrightarrow {SG} } \right| \Rightarrow SG = \frac{{\left| {\overrightarrow F } \right|}}{3} = 10.\)
Vậy \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {SA} } \right| = 2\frac{{SG}}{{\sqrt 3 }} = \frac{{20}}{{\sqrt 3 }} \approx 11,5\left( {\rm{N}} \right){\rm{.}}\)
Đáp án: 11,5.
Lời giải
Chọn hệ trục tọa độ Oxyz với gốc O đặt tại điểm xuất phát của máy bay, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất sao cho trục Ox hướng về phía Nam, trục Oy hướng về phía Đông và trục Oz hướng thẳng đứng lên trời, đơn vị đo lấy theo kilômét.
Khi đó tọa độ của máy bay là điểm \(A\left( { - 55; - 20;1,5} \right)\).
Khoảng cách của chiếc máy bay với vị trí tại điểm xuất phát bằng:
\(OA = \sqrt {{{\left( { - 55} \right)}^2} + {{\left( { - 20} \right)}^2} + 1,{5^2}} \approx 58,5\left( {{\rm{km}}} \right)\).
Đáp án: 58,5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0\).
B. \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {DA} \).
C. \(\overrightarrow {AB} + \overrightarrow {DC} - \overrightarrow {DB} = \overrightarrow {CA} \).
D. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.