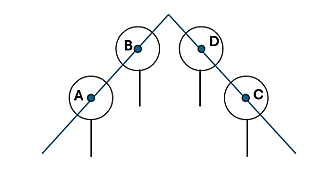
Năm 2011, kỹ sư Nguyễn Trí Hiếu, người Quảng Ngãi, đã sáng chế ra chiếc xe đu dây phục vụ công nhân điện lực di chuyển trên dây điện cao thế. Khi ở vị trí cân bằng, chiếc xe và đường dây điện sẽ cùng nằm trên một mặt phẳng vuông góc với mặt đất. Xe được cấu tạo bởi khung xe có gắn hai Puly tại vị trí A và B cách mặt đất lần lượt là 20 m và 19,9 m (như hình). Xe đu dây di chuyển giống xe đạp, được kết hợp dây xích, líp, đĩa, bàn đạp, phanh; bàn đạp đặt tại vị trí C.
Chọn hệ trục tọa độ \(Oxyz\) sao cho mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất (mỗi đơn vị độ dài trong không gian \(Oxyz\) tương ứng với 1m trên thực tế); tọa độ các điểm \(A,B,C\) lần lượt là \(\left( {7;5;20} \right)\;\), \(\left( {7;5,5;19,9} \right),\left( {7;5;19} \right)\).
a) Một vectơ chỉ phương của đường thẳng \(AB\) là \(\vec u = \left( {0;5;1} \right)\).
b) Khi người thợ điện di chuyển đến vị trí điểm \(D\) cách mặt đất 18 m thì tọa độ điểm \(D\) là \(D\left( {7; - 5;18} \right)\).
c) Phương trình mặt phẳng \(\left( {ABC} \right)\) là \(x = 7\).
d) Khoảng cách từ Puly tại \(A\;\) đến bàn đạp tại \(C\) là \(1,03\) m.
Năm 2011, kỹ sư Nguyễn Trí Hiếu, người Quảng Ngãi, đã sáng chế ra chiếc xe đu dây phục vụ công nhân điện lực di chuyển trên dây điện cao thế. Khi ở vị trí cân bằng, chiếc xe và đường dây điện sẽ cùng nằm trên một mặt phẳng vuông góc với mặt đất. Xe được cấu tạo bởi khung xe có gắn hai Puly tại vị trí A và B cách mặt đất lần lượt là 20 m và 19,9 m (như hình). Xe đu dây di chuyển giống xe đạp, được kết hợp dây xích, líp, đĩa, bàn đạp, phanh; bàn đạp đặt tại vị trí C.
Chọn hệ trục tọa độ \(Oxyz\) sao cho mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất (mỗi đơn vị độ dài trong không gian \(Oxyz\) tương ứng với 1m trên thực tế); tọa độ các điểm \(A,B,C\) lần lượt là \(\left( {7;5;20} \right)\;\), \(\left( {7;5,5;19,9} \right),\left( {7;5;19} \right)\).
a) Một vectơ chỉ phương của đường thẳng \(AB\) là \(\vec u = \left( {0;5;1} \right)\).
b) Khi người thợ điện di chuyển đến vị trí điểm \(D\) cách mặt đất 18 m thì tọa độ điểm \(D\) là \(D\left( {7; - 5;18} \right)\).
c) Phương trình mặt phẳng \(\left( {ABC} \right)\) là \(x = 7\).
d) Khoảng cách từ Puly tại \(A\;\) đến bàn đạp tại \(C\) là \(1,03\) m.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Sai. Ta có \(\overrightarrow {AB} = \left( {0;0,5; - 0,1} \right)\) nên một vectơ chỉ phương của đường thẳng \(AB\) là \(\vec u = \left( {0;5; - 1} \right).\)
b) Sai. Ta có đường thẳng \(AB\) đi qua \(A\left( {7;5;20} \right)\) và có vectơ chỉ phương \(\vec u = \left( {0;5; - 1} \right)\) nên có phương trình tham số là \(\left\{ {\begin{array}{*{20}{c}}{x = 7}\\{y = 5 + 5t}\\{z = 20 - t}\end{array}} \right.\).
Mặt đất là \(\left( {Oxy} \right):z = 0\), điểm \(D\left( {7;5 + 5t;20 - t} \right) \in AB\) cách mặt đất 18 m hay
\(d\left( {D,\left( {Oxy} \right)} \right) = 18 \Leftrightarrow \left| {20 - t} \right| = 18 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 2}\\{t = 38}\end{array}} \right.\).
Khi đó \(D\left( {7;15;18} \right)\) (điểm \(D\left( {7;195; - 18} \right)\) loại do cao độ của dây không âm).
c) Đúng. Mặt phẳng \(\left( {ABC} \right)\) đi qua \(A\left( {7;5;20} \right)\) và có vectơ pháp tuyến \(\left[ {\overrightarrow {AB} ,\;\overrightarrow {AC} } \right] = \left( { - 0,5;0;0} \right)\) hay \(\vec n = \left( {1;0;0} \right)\). Suy ra phương trình mặt phẳng \(\left( {ABC} \right):\;x = 7\).
d) Sai. Ta có \(AC = \sqrt {{{\left( {7 - 7} \right)}^2} + {{\left( {5 - 5} \right)}^2} + {{\left( {19 - 20} \right)}^2}} = 1\) (m).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \[M = AB \cap CD\] (là điểm hai viên đạn va chạm nhau) khi đó \[AM = 150\,{\rm{m}}\;(1)\].
Ta có \[\overrightarrow {AB} = \left( {1\,;2\,;2} \right)\] là vectơ chỉ phương của đường thẳng \[AB\].
Phương trình tham số đường thẳng \[AB\] là \[\left\{ {\begin{array}{*{20}{c}}{x = 5 + t}\\{y = 7 + 2t}\\{z = 10 + 2t}\end{array}} \right.\quad (t \in \mathbb{R})\].
Do \[M \in AB \Rightarrow M\left( {5 + t;7 + 2t;10 + 2t} \right)\]. Từ (1) ta có \[\sqrt {{t^2} + 4{t^2} + 4{t^2}} = 150 \Leftrightarrow \left| t \right| = 50\].
Với \[t = 50 \Rightarrow M\left( {55;107;110} \right)\] và với \[t = - 50 \Rightarrow M\left( { - 45; - 93; - 90} \right)\].
Vì cao độ điểm \[D\] dương nên cao độ của điểm \[M\] dương\[ \Rightarrow M\left( {55\,;107\,;110} \right)\].
Vậy vectơ chỉ phương của đường thẳng \[CD\] là \[\overrightarrow {CM} = \left( {40;90;105} \right)\].
Khi đó, phương trình tham số đường thẳng \[CD\] là \[\left\{ {\begin{array}{*{20}{c}}{x = 15 + 40t'}\\{y = 17 + 90t'}\\{z = 5 + 105t'}\end{array}} \right.\quad (t' \in \mathbb{R})\].
Mà điểm \[D\] cách mặt đất \[26\,{\rm{m}}\] nên điểm \[D\] có cao độ bằng \[26\]
\[ \Rightarrow \]\[5 + 105t' = 26 \Leftrightarrow t' = \frac{1}{5} \Rightarrow D\left( {23\,;35\,;26} \right)\]. \[C\left( {15\,;17\,;5} \right)\]
Khi đó độ dài \[CD = \sqrt {{{\left( {15 - 23} \right)}^2} + {{\left( {17 - 35} \right)}^2} + {{\left( {5 - 26} \right)}^2}} \approx 28,8\,\,{\rm{(m)}}.\]
Đáp án: 28,8.
Lời giải
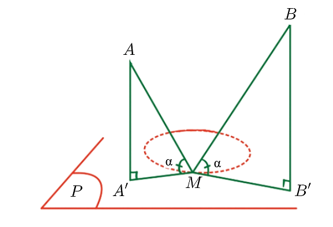
Gọi \(A',B'\) lần lượt là hình chiếu vuông góc của \(A,B\) lên mặt phẳng \(\left( P \right)\).
Góc tạo bởi \(MA\) với mặt vườn và góc tạo bởi \(MB\) với mặt vườn phải luôn bằng nhau.
Nên ta có \( \Rightarrow \frac{{MA}}{{MB}} = \frac{{AA'}}{{BB'}} = \frac{{d\left( {A,\left( P \right)} \right)}}{{d\left( {B,\left( P \right)} \right)}}\).
Mà \(d\left( {A,\left( P \right)} \right) = \frac{{\left| {2 \cdot 40 + 2 \cdot \left( { - 40} \right) - 12 - 12} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = 8\); \[d\left( {B,\left( P \right)} \right) = \frac{{\left| {2 \cdot \left( { - 40} \right) + 2 \cdot 50 - 38 - 12} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = 10\].
\( \Rightarrow \frac{{MA}}{{MB}} = \frac{8}{{10}} = \frac{4}{5} \Rightarrow 5MA = 4MB\). Gọi \(M\left( {x;y;z} \right)\). Khi đó, ta được:
\(25 \cdot \left[ {{{\left( {x - 40} \right)}^2} + {{\left( {y + 40} \right)}^2} + {{\left( {z - 12} \right)}^2}} \right] = 16 \cdot \left[ {{{\left( {x + 40} \right)}^2} + {{\left( {y - 50} \right)}^2} + {{\left( {z - 38} \right)}^2}} \right]\).
Rút gọn ta được phương trình mặt cầu \(\left( S \right)\) chứa các điểm \(M\) thoả mãn yêu cầu kĩ thuật:
\({x^2} + {y^2} + {z^2} - \frac{{3280}}{9}x + 400y + \frac{{616}}{9}z - \frac{{5104}}{9} = 0\).
Đồng thời, vì điểm \(M\) nằm trên mặt vườn nên \(M \in \left( P \right):\;{\mkern 1mu} 2x + 2y - z - 12 = 0\).
Như vậy, tập hợp điểm \(M\) cần tìm là giao tuyến của mặt cầu \(\left( S \right)\) và mặt phẳng \(\left( P \right)\), tức là một đường tròn \(\left( C \right)\).
Gọi \(I\) là tâm mặt cầu \(\left( S \right)\), ta được: \(I\left( {\frac{{1640}}{9}; - 200; - \frac{{308}}{9}} \right)\).
Bán kính của mặt cầu \(\left( S \right)\):
\(R = \sqrt {{a^2} + {b^2} + {c^2} - d} = \sqrt {{{\left( {\frac{{1640}}{9}} \right)}^2} + {{\left( { - 200} \right)}^2} + {{\left( {\frac{{ - 308}}{9}} \right)}^2} + \frac{{5104}}{9}} = \sqrt {\frac{{6070400}}{{81}}} \).
Khoảng cách từ tâm \(I\) đến mặt phẳng \(\left( P \right)\): \(d = \frac{{\left| {2 \cdot \frac{{1640}}{9} + 2 \cdot \left( { - 200} \right) + \frac{{308}}{9} - 12} \right|}}{{\sqrt {4 + 4 + 1} }} = \frac{{40}}{9}\).
Bán kính đường tròn giao tuyến \(\left( C \right)\): \(r = \sqrt {{R^2} - {d^2}} = \sqrt {\frac{{6068800}}{{81}}} \).
Vậy độ dài đường ray là chu vi đường tròn \(\left( C \right)\): \(l = 2\pi r \approx 1720\;{\rm{(m)}}\).
Đáp án: 1720.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo