Trong một đợt diễn tập quốc phòng, hai người ở hai vị trí khác nhau cùng ngắm bắn một mục tiêu cố định trên không. Người ta gắn một hệ trục tọa độ \[Oxyz\] (đơn vị trên mỗi trục tính theo mét), mặt phẳng \[\left( {Oxy} \right)\] trùng mặt đất. Người thứ nhất bắn một viên đạn đi qua hai điểm \[A\left( {5\,;7\,;10} \right)\] và \[B\left( {6\,;9\,;12} \right)\]. Người thứ hai bắn một viên đạn đi qua hai điểm \[C\left( {15\,;17\,;5} \right)\] và \[D\](điểm \[D\] ở độ cao \[26\,{\rm{m}}\] so với mặt đất). Biết rằng sau một thời gian rời khỏi nòng súng, hai viên đạn va chạm nhau tại một vị trí cách \[A\] một khoảng bằng \[150\,{\rm{m}}\] (tham khảo hình vẽ).
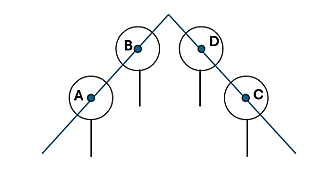
Hỏi \[D\] cách \[C\] một khoảng bao nhiêu mét? (Kết quả làm tròn đến hàng phần chục).
Trong một đợt diễn tập quốc phòng, hai người ở hai vị trí khác nhau cùng ngắm bắn một mục tiêu cố định trên không. Người ta gắn một hệ trục tọa độ \[Oxyz\] (đơn vị trên mỗi trục tính theo mét), mặt phẳng \[\left( {Oxy} \right)\] trùng mặt đất. Người thứ nhất bắn một viên đạn đi qua hai điểm \[A\left( {5\,;7\,;10} \right)\] và \[B\left( {6\,;9\,;12} \right)\]. Người thứ hai bắn một viên đạn đi qua hai điểm \[C\left( {15\,;17\,;5} \right)\] và \[D\](điểm \[D\] ở độ cao \[26\,{\rm{m}}\] so với mặt đất). Biết rằng sau một thời gian rời khỏi nòng súng, hai viên đạn va chạm nhau tại một vị trí cách \[A\] một khoảng bằng \[150\,{\rm{m}}\] (tham khảo hình vẽ).

Hỏi \[D\] cách \[C\] một khoảng bao nhiêu mét? (Kết quả làm tròn đến hàng phần chục).
Quảng cáo
Trả lời:
Gọi \[M = AB \cap CD\] (là điểm hai viên đạn va chạm nhau) khi đó \[AM = 150\,{\rm{m}}\;(1)\].
Ta có \[\overrightarrow {AB} = \left( {1\,;2\,;2} \right)\] là vectơ chỉ phương của đường thẳng \[AB\].
Phương trình tham số đường thẳng \[AB\] là \[\left\{ {\begin{array}{*{20}{c}}{x = 5 + t}\\{y = 7 + 2t}\\{z = 10 + 2t}\end{array}} \right.\quad (t \in \mathbb{R})\].
Do \[M \in AB \Rightarrow M\left( {5 + t;7 + 2t;10 + 2t} \right)\]. Từ (1) ta có \[\sqrt {{t^2} + 4{t^2} + 4{t^2}} = 150 \Leftrightarrow \left| t \right| = 50\].
Với \[t = 50 \Rightarrow M\left( {55;107;110} \right)\] và với \[t = - 50 \Rightarrow M\left( { - 45; - 93; - 90} \right)\].
Vì cao độ điểm \[D\] dương nên cao độ của điểm \[M\] dương\[ \Rightarrow M\left( {55\,;107\,;110} \right)\].
Vậy vectơ chỉ phương của đường thẳng \[CD\] là \[\overrightarrow {CM} = \left( {40;90;105} \right)\].
Khi đó, phương trình tham số đường thẳng \[CD\] là \[\left\{ {\begin{array}{*{20}{c}}{x = 15 + 40t'}\\{y = 17 + 90t'}\\{z = 5 + 105t'}\end{array}} \right.\quad (t' \in \mathbb{R})\].
Mà điểm \[D\] cách mặt đất \[26\,{\rm{m}}\] nên điểm \[D\] có cao độ bằng \[26\]
\[ \Rightarrow \]\[5 + 105t' = 26 \Leftrightarrow t' = \frac{1}{5} \Rightarrow D\left( {23\,;35\,;26} \right)\]. \[C\left( {15\,;17\,;5} \right)\]
Khi đó độ dài \[CD = \sqrt {{{\left( {15 - 23} \right)}^2} + {{\left( {17 - 35} \right)}^2} + {{\left( {5 - 26} \right)}^2}} \approx 28,8\,\,{\rm{(m)}}.\]
Đáp án: 28,8.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
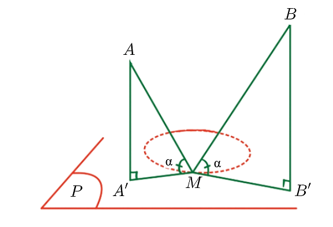
Gọi \(A',B'\) lần lượt là hình chiếu vuông góc của \(A,B\) lên mặt phẳng \(\left( P \right)\).
Góc tạo bởi \(MA\) với mặt vườn và góc tạo bởi \(MB\) với mặt vườn phải luôn bằng nhau.
Nên ta có \( \Rightarrow \frac{{MA}}{{MB}} = \frac{{AA'}}{{BB'}} = \frac{{d\left( {A,\left( P \right)} \right)}}{{d\left( {B,\left( P \right)} \right)}}\).
Mà \(d\left( {A,\left( P \right)} \right) = \frac{{\left| {2 \cdot 40 + 2 \cdot \left( { - 40} \right) - 12 - 12} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = 8\); \[d\left( {B,\left( P \right)} \right) = \frac{{\left| {2 \cdot \left( { - 40} \right) + 2 \cdot 50 - 38 - 12} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = 10\].
\( \Rightarrow \frac{{MA}}{{MB}} = \frac{8}{{10}} = \frac{4}{5} \Rightarrow 5MA = 4MB\). Gọi \(M\left( {x;y;z} \right)\). Khi đó, ta được:
\(25 \cdot \left[ {{{\left( {x - 40} \right)}^2} + {{\left( {y + 40} \right)}^2} + {{\left( {z - 12} \right)}^2}} \right] = 16 \cdot \left[ {{{\left( {x + 40} \right)}^2} + {{\left( {y - 50} \right)}^2} + {{\left( {z - 38} \right)}^2}} \right]\).
Rút gọn ta được phương trình mặt cầu \(\left( S \right)\) chứa các điểm \(M\) thoả mãn yêu cầu kĩ thuật:
\({x^2} + {y^2} + {z^2} - \frac{{3280}}{9}x + 400y + \frac{{616}}{9}z - \frac{{5104}}{9} = 0\).
Đồng thời, vì điểm \(M\) nằm trên mặt vườn nên \(M \in \left( P \right):\;{\mkern 1mu} 2x + 2y - z - 12 = 0\).
Như vậy, tập hợp điểm \(M\) cần tìm là giao tuyến của mặt cầu \(\left( S \right)\) và mặt phẳng \(\left( P \right)\), tức là một đường tròn \(\left( C \right)\).
Gọi \(I\) là tâm mặt cầu \(\left( S \right)\), ta được: \(I\left( {\frac{{1640}}{9}; - 200; - \frac{{308}}{9}} \right)\).
Bán kính của mặt cầu \(\left( S \right)\):
\(R = \sqrt {{a^2} + {b^2} + {c^2} - d} = \sqrt {{{\left( {\frac{{1640}}{9}} \right)}^2} + {{\left( { - 200} \right)}^2} + {{\left( {\frac{{ - 308}}{9}} \right)}^2} + \frac{{5104}}{9}} = \sqrt {\frac{{6070400}}{{81}}} \).
Khoảng cách từ tâm \(I\) đến mặt phẳng \(\left( P \right)\): \(d = \frac{{\left| {2 \cdot \frac{{1640}}{9} + 2 \cdot \left( { - 200} \right) + \frac{{308}}{9} - 12} \right|}}{{\sqrt {4 + 4 + 1} }} = \frac{{40}}{9}\).
Bán kính đường tròn giao tuyến \(\left( C \right)\): \(r = \sqrt {{R^2} - {d^2}} = \sqrt {\frac{{6068800}}{{81}}} \).
Vậy độ dài đường ray là chu vi đường tròn \(\left( C \right)\): \(l = 2\pi r \approx 1720\;{\rm{(m)}}\).
Đáp án: 1720.
Lời giải
Với hệ trục tọa độ \(Oxyz\) cho trước (đơn vị: mét), tọa độ của \(A,\,B\) lần lượt là \(A\left( {3;\,2,5;\,15} \right)\) và\(B\left( {21;\,27,5;\,10} \right)\).
Đường thẳng \(AB\)đi qua \(A\left( {3;\,2,5;\,15} \right)\) và nhận \(\overrightarrow {AB} = \left( {18;\,25; - \,5} \right)\) là vectơ chỉ phương nên có phương trình: \(\left\{ \begin{array}{l}x = 3 + 18t\\y = 2,5 + 25t\\z = 15 - 5t\end{array} \right.\).
Khi du khách ở độ cao \(12\,{\rm{m}}\) thì \(z = 12 \Rightarrow 15 - 5t = 12 \Leftrightarrow t = \frac{3}{5}\). Do đó \(x = 13,8;\,\,y = 17,5\).
Vậy tọa độ của du khách lúc đó là \(M\left( {13,8;\,17,5;\,12} \right) \Rightarrow a + b + c = 43,3\).
Đáp án: 43,3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

