(1,0 điểm) Cho số hữu tỉ \(y = \frac{{4t - 8}}{5}\) (\(t\) là số nguyên). Với giá trị nào của \(a\) thì:
(a) \(y\) là số nguyên?
(b) \(y\) không là số hữu tỉ âm cũng không là số hữu tỉ dương?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có: \(4t - 8 = 4\left( {t - 2} \right)\).
Với \(y\) là số nguyên thì \(\left( {4t - 8} \right)\,\, \vdots \,\,5\) hay \(4\left( {t - 2} \right)\,\, \vdots \,\,5\).
Vì ƯCLN(4, 5) = 1 nên \(\left( {t - 2} \right)\,\, \vdots \,\,5\) hay \(t - 2 = 5k\) \(\left( {k \in \mathbb{Z}} \right)\).
Suy ra \(t = 5k + 2\).
Vậy để \(y\) là số nguyên thì \(t\) chia 5 dư 2.
b) Với\(y\) không là số hữu tỉ âm cũng không là số hữu tỉ dương nên \(y = 0\).
Khi đó \(4t - 8 = 0\) suy ra hay .
Vậy để không là số hữu tỉ âm cũng không là số hữu tỉ dương thì .
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) \[\frac{4}{3}:\frac{{ - 5}}{6} + \frac{{11}}{2} = \frac{{ - 8}}{5} + \frac{{11}}{2} = \frac{{39}}{{10}}\];
b) \(\frac{3}{4}\,\,.\,\,\frac{{ - 4}}{7} + \frac{{ - 4}}{7}\,\,.\,\,\frac{5}{4} = \frac{{ - 4}}{7}\,\,.\,\,\left( {\frac{5}{4} + \frac{3}{4}} \right) = \frac{{ - 4}}{7}\,\,.\,\,2 = \frac{{ - 8}}{7}\);
c) \[\sqrt {0,81} \,\,.\,\,{\left( {\frac{{ - 1}}{3}} \right)^2} - \sqrt {\frac{1}{{196}}} \,\,.\,\,{( - 7)^3} = 0,9\,\,.\,\,\frac{1}{9} + \frac{1}{{14}}\,\,.\,\,{7^3}\]
\[ = 0,9\,\,.\,\,\frac{1}{9} + \frac{1}{{14}}\,\,.\,\,{7^3} = \frac{1}{{10}} + \frac{{{7^3}}}{{7\,\,.\,\,2}} = \frac{1}{{10}} + \frac{{49}}{2} = \frac{{123}}{5}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
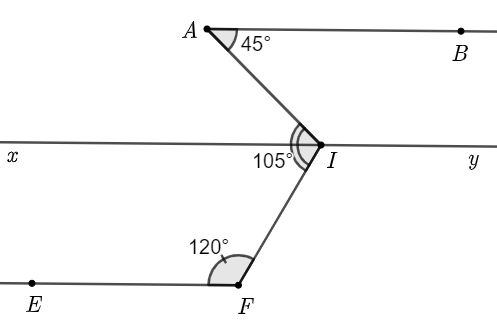
b) Vì \(AB\parallel xy\) nên \(\widehat {BAI} = \widehat {AIx} = 45^\circ \) (hai góc so le trong).
Ta có \(\widehat {AIF} = \widehat {AIx} + \widehat {FIx}\).
Suy ra \(\widehat {FIx} = \widehat {AIF} - \widehat {AIx} = 105^\circ - 45^\circ = 60^\circ \).
Vì \(\widehat {FIx}\) và \(\widehat {FIy}\) là hai góc kề bù nên \(\widehat {FIx} + \widehat {FIy} = 180^\circ \).
Suy ra \(\widehat {FIy} = 180^\circ - \widehat {FIx} = 180^\circ - 60^\circ = 120^\circ \).
Vậy \(\widehat {FIx} = 60^\circ \); \(\widehat {FIy} = 120^\circ \).
c) Ta thấy \(\widehat {FIy} = \widehat {EFI} = 120^\circ \) mà \(\widehat {FIy}\) và \(\widehat {EFI}\) ở vị trí so le trong.
Do đó\[AB\parallel EF\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
\(\frac{7}{5}\)
\(\frac{{ - 2}}{5}\)
\(\frac{9}{5}\)
\(\frac{3}{5}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\(\frac{4}{6}\)
\(\frac{{ - 6}}{9}\)
\(\frac{{ - 4}}{9}\)
\(\frac{{ - 4}}{{ - 6}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
\[\sqrt 7 \]
\(\sqrt {36} \)
\(\sqrt {21} \)
\(\sqrt {19} \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập