Khẳng định nào sau đúng?
Số đối của số hữu tỉ \(a\) là số \( - a\)
Số hữu tỉ 0 không có số đối
Hai số hữu tỉ \(a\) và \(b\) đối nhau nếu \(a - b = 0\)
Mỗi một số hữu tỉ có hai số đối.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
Số đối của số hữu tỉ \(a\) là số \( - a\);
B sai vì số đối của 0 là 0;
C sai vì nếu \(a\) và \(b\) là hai số đối nhau thì \(a + b = 0\);
D sai vì mỗi số hữu tỉ chỉ có một số đối.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
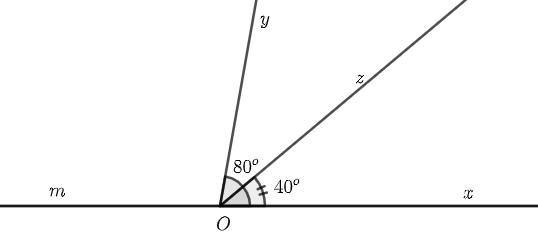
a) Vì \(Oz\) nằm giữa hai tia \(Ox,\,\,Oy\) nên \(\widehat {xOz} + \widehat {zOy} = \widehat {xOy}\)
Hay \(40^\circ + \widehat {zOy} = 80^\circ \).
Suy ra \(\widehat {zOy} = 80^\circ - 40^\circ = 40^\circ \).
Vậy \(\widehat {zOy} = 40^\circ \).
Ta có \(Oz\) nằm giữa hai tia \(Ox,\,\,Oy\) và \(\widehat {xOz} = \widehat {zOy} = \frac{{\widehat {xOy}}}{2}\).
Do đó tia \(Oz\) là tia phân giác của \(\widehat {xOy}\).
b) Vì \(Om\)là tia đối của tia \(Ox\) nên \(\widehat {mOz}\) và \(\widehat {zOx}\) là hai góc kề bù.
Khi đó, ta có \(\widehat {mOz} + \widehat {zOx} = 180^\circ \)
Suy ra \[\widehat {mOz} = 180^\circ - \widehat {zOx} = 180^\circ - 40^\circ = 140^\circ \].
Vậy \(\widehat {mOz} = 140^\circ \).
Lời giải
Vì \(\frac{1}{4}\) số hàng nhập về không đảm bảo chất lượng bán với giá thấp hơn 15% giá nhập vào nên \(\frac{1}{4}\) số hàng đó, số tiền cô Phương bị lỗ:
\(\frac{1}{4}\,\,.\,\,80\,\,.\,\,15\% = 3\) (triệu đồng).
Vì số hàng còn lại bán với giá cao hơn 30% giá nhập vào nên \(\frac{3}{4}\) số hàng đó, số tiền cô Phương bị lãi:
\(\frac{3}{4}\,\,.\,\,80\,\,.\,\,30\% = 18\) (triệu đồng).
Cả lô hàng mới của cô Phương lãi số tiền là:
\(18 - 3 = 15\) (triệu đồng).
Vậy cả lô hàng mới của cô Phương lãi 15 triệu đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Điểm \(D\)
Điểm \(B\)
Điểm \(C\)
Điểm \(A\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.