Khẳng định nào sau đây đúng?
A.
Hai góc có tổng số đo là \(180^\circ \) là hai góc kề bù
B.
Hai góc kề bù là hai góc vừa kề nhau vừa bù nhau
C.
Hai góc có một cạnh chung là hai góc kề bù
D.
Hai góc kề bù là hai góc có một cạnh chung và có tổng số đo là \(90^\circ \).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Khẳng định đúng là: Hai góc kề bù là hai góc vừa kề nhau vừa bù nhau.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
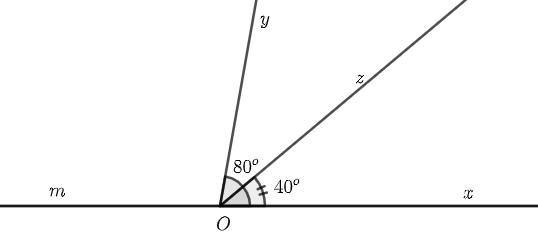
a) Vì \(Oz\) nằm giữa hai tia \(Ox,\,\,Oy\) nên \(\widehat {xOz} + \widehat {zOy} = \widehat {xOy}\)
Hay \(40^\circ + \widehat {zOy} = 80^\circ \).
Suy ra \(\widehat {zOy} = 80^\circ - 40^\circ = 40^\circ \).
Vậy \(\widehat {zOy} = 40^\circ \).
Ta có \(Oz\) nằm giữa hai tia \(Ox,\,\,Oy\) và \(\widehat {xOz} = \widehat {zOy} = \frac{{\widehat {xOy}}}{2}\).
Do đó tia \(Oz\) là tia phân giác của \(\widehat {xOy}\).
b) Vì \(Om\)là tia đối của tia \(Ox\) nên \(\widehat {mOz}\) và \(\widehat {zOx}\) là hai góc kề bù.
Khi đó, ta có \(\widehat {mOz} + \widehat {zOx} = 180^\circ \)
Suy ra \[\widehat {mOz} = 180^\circ - \widehat {zOx} = 180^\circ - 40^\circ = 140^\circ \].
Vậy \(\widehat {mOz} = 140^\circ \).
Lời giải
a) \(\frac{1}{4}x - \frac{1}{3} = - \frac{5}{9}\)
\(\frac{1}{4}x = - \frac{5}{9} + \frac{1}{3}\)
\(\frac{1}{4}x = - \frac{2}{9}\)
\(x = - \frac{2}{9}:\frac{1}{4}\)
\(x = - \frac{8}{9}\)
Vậy \(x = - \frac{8}{9}\).
b) \({2^{x - 3}} - {3.2^x} = - 92\)
\(\frac{{{2^x}}}{{{2^3}}} - {3.2^x} = - 92\)
\({2^x}.\left( {\frac{1}{8} - 3} \right) = - 92\)
\({2^x}.\frac{{ - 23}}{8} = - 92\)
\({2^x} = 32\)
\({2^x} = {2^5}\)
Suy ra \(x = 5\)
Vậy \(x = 5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
\({S_{xq}} = 2\,\,.\,\,\left( {a + b} \right)\,\,.\,\,h\)
\({S_{xq}} = 2\,\,.\,\,\left( {a + h} \right)\,\,.\,\,b\)
\({S_{xq}} = 2\,\,.\,\,\left( {a + b + h} \right)\)
\({S_{xq}} = \left( {a + b} \right)\,\,.\,\,h\) .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.
\( - 1,25 \in \mathbb{Q}\)
B.
\(\frac{2}{9} \notin \mathbb{Z}\)
C.
\( - 48 \in \mathbb{N}\)
D.
\[\frac{{ - 5}}{7} \in \mathbb{Q}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.
30 cm3
B.
15 cm3
C.
30 cm2
D.
15 cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo