Cho \(\Delta ABC\) có \(AE\;\left( {E \in BC} \right)\) là đường phân giác của tam giác. Gọi \(I\) là điểm nằm trên cạnh \(AB\) sao cho \(\frac{{AI}}{{BI}} = \frac{{AC}}{{BC}}.\) Gọi \(D\) là giao điểm của \(AE\) và \(CI.\) Khi đó:
A. \(\widehat {ABD} = \frac{2}{3}\widehat {DBC}.\)
B. \(\widehat {ABD} = \frac{4}{5}\widehat {DBC}.\)
C. \(\widehat {ABD} = \frac{3}{4}\widehat {DBC}.\)
D. \(\widehat {ABD} = \widehat {DBC}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
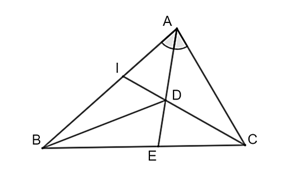
\(\Delta ABC\) có \(\frac{{AI}}{{BI}} = \frac{{AC}}{{BC}}\) nên \(CI\) là tia phân giác của \(\widehat {ACB}.\)
Vì \(D\) là giao điểm của hai đường phân giác \(AE\) và \(CI\) của \(\Delta ABC\) nên \(BD\) là đường phân giác của \(\widehat {ABC}\) trong \(\Delta ABC.\) Do đó, \(\widehat {ABD} = \widehat {DBC}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(x = 62\;{\rm{cm}}.\)
B. \(x = 72\;{\rm{cm}}.\)
C. \(x = 70\;{\rm{cm}}.\)
D. \(x = 60\;{\rm{cm}}.\)
Câu 2
A. \(BC = 20\;{\rm{cm}}{\rm{.}}\)
B. \(BC = 20,4\;{\rm{cm}}{\rm{.}}\)
C. \(BC = 20,8\;{\rm{cm}}{\rm{.}}\)
D. \(BC = 20,6\;{\rm{cm}}{\rm{.}}\)
Lời giải
Đáp án đúng là: C
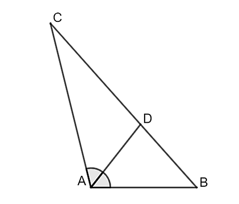
Vì \(AD\) là đường phân giác của \(\Delta ABC\) nên \(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}}.\) Suy ra: \(DC = \frac{{AC \cdot BD}}{{AB}} = \frac{{16 \cdot 8}}{{10}} = 12,8\;\left( {{\rm{cm}}} \right).\)
Do đó, \(BC = CD + DB = 12,8 + 8 = 20,8\;\left( {{\rm{cm}}} \right).\) Vậy \(BC = 20,8\;{\rm{cm}}{\rm{.}}\)
Câu 3
A. \(\widehat {DAC} = 60^\circ .\)
B. \(\widehat {DAC} = 40^\circ .\)
C. \(\widehat {DAC} = 50^\circ .\)
D. \(\widehat {DAC} = 45^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) \(\frac{{CM}}{{CB}} = \frac{1}{2}.\)
Đúng
Sai
b) \(BE = 2EM.\)
Đúng
Sai
c) Thời gian bạn Dũng đi gấp hai lần thời gian bạn Minh đi khi hai bạn gặp nhau tại điểm \(E.\)
Đúng
Sai
d) Bạn Dũng cần xuất phát lúc \(12\) giờ thì hai bạn gặp nhau tại điểm \(E\) lúc \(13\) giờ \(30\) phút.
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}}.\)
B. \(\frac{{AB}}{{AC}} = \frac{{DC}}{{DB}}.\)
C. \(\frac{{AB}}{{AC}} = \frac{{BD}}{{BC}}.\)
D. \(\frac{{AB}}{{AC}} = \frac{{DC}}{{BC}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập