Cho hình tứ diện \[ABCD\] có tất cả các cạnh bằng \[6.\] Gọi \[M,N\] lần lượt là trung điểm của \[CA,CB.\] \[P\] là điểm trên cạnh \[BD\] sao cho \[BP = 2PD.\] Gọi \[(H)\] là hình giới hạn bởi giao tuyến của mặt phẳng \[(MNP)\] với các mặt của tứ diện \[ABCD.\] Tính diện tích hình \[(H)\] (kết quả làm tròn đến hàng phần trăm).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
8,93
Đáp án: 8,93.
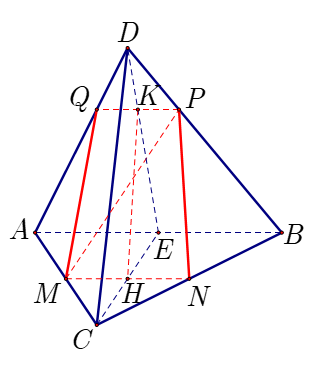
Theo đề bài ta có tất cả các mặt của tứ diện là tam giác đều có cạnh bằng \(6.\)
Ta có: \(P \in (MNP),P \in BD \subset (ABD) \Rightarrow P \subset (MNP) \cap (ABD).\)
Mặt khác:
Suy ra \((MNP) \cap (ABD) = d\) là đường thẳng qua \(P\) và song song với \(AB\).
Trong mặt phẳng \((ABD),\) gọi \(Q = d \cap AD\). Khi đó, thiết diện cần tính diện tích là tứ giác \(MNPQ.\)
Ta có \(MN\parallel AB,PQ\parallel AB \Rightarrow MN\parallel PQ \Rightarrow MNPQ\) là hình thang.
Mặt khác :
\(MN\parallel AB \Rightarrow AM = BN;PQ\parallel AB \Rightarrow AQ = BP;\widehat {MAQ} = \widehat {NBP} = 60^\circ \Rightarrow MQ = NP\)
Hay \(MNPQ\) là hình thang cân.
Gọi \(E\) là trung điểm của \(AB;H = AE \cap MN,K = DE \cap PQ.\)
Ta có : \(AB \bot AE(HE),AB \bot DE(EK) \Rightarrow AB \bot HK,MN\parallel AB \Rightarrow HK \bot MN\)
\({S_{MNPQ}} = \frac{{MN + PQ}}{2}.HK\)
\(MN = \frac{1}{2}AB = 3;PQ = \frac{1}{3}AB = 2.\)
\(EC = ED = \frac{{AB\sqrt 3 }}{2} = 3\sqrt 3 ;EH = \frac{1}{2}EC = \frac{{3\sqrt 3 }}{2};EK = \frac{2}{3}ED = 2\sqrt 3 \)
\(\begin{array}{l}{\rm{ }}H{K^2} = E{H^2} + E{K^2} - 2EH.EK.\cos \widehat {CED}\\ & = E{H^2} + E{K^2} - 2EH.EK.\frac{{E{C^2} + E{D^2} - C{D^2}}}{{2EC.ED}} = \frac{{51}}{4}.\\ \Rightarrow HK = \frac{{\sqrt {51} }}{2}\end{array}\)
Vậy \({S_{MNPQ}} = \frac{{3 + 2}}{2}.\frac{{\sqrt {51} }}{2} = \frac{{5\sqrt {51} }}{4} \approx 8,93.\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Có 45 quả cầu nên số lượng quả cầu được đánh số chẵn là 22 và số lượng quả cầu đánh số lẻ là 23.
a) Đúng. Số cách lấy được cả 3 quả cầu đánh số chẵn là \(C_{22}^3 = 1540\).
b) Sai. Số cách lấy 3 quả tùy ý là \(n\left( \Omega \right) = C_{45}^3 = 14190\).
Ta chia các quả cầu thành các nhóm \({S_0};{S_1};{S_2};{S_3}\) là các nhóm chứa các quả cầu lần lượt có các số dư như sau:
\({S_0}\) gồm 5 số chia hết cho 8
\({S_1}\) gồm 11 số chia hết cho 2 mà không chia hết cho 4
\({S_2}\) gồm 6 số chia hết cho 4 mà không chia hết cho 8
\({S_3}\) gồm 23 số lẻ.
Gọi \(A\) là biến cố: “tích 3 số ghi trên 3 quả cầu là một số chia hết cho 8”.
Ta đi tính \(n\left( {\overline A } \right)\).
Để tích 3 số không chia hết cho 8 thì xảy ra các trường hợp:
3 số thuộc \({S_3}\).
1 số thuộc \({S_1}\) và 2 số thuộc \({S_3}\).
1 số thuộc \({S_2}\) và 2 số thuộc \({S_3}\).
2 số thuộc \({S_1}\) và 1 số thuộc \({S_3}\).
\(n\left( {\overline A } \right) = C_{23}^3 + C_{23}^2\left( {C_{11}^1 + C_6^1} \right) + C_{23}^1C_{11}^2 = 1771 + 4301 + 1265 = 7337\).
Suy ra \(P\left( A \right) = 1 - P\left( {\overline A } \right) = \frac{{623}}{{1290}}\).
c) Sai. Để chọn được 3 số có tổng là số lẻ thì xảy ra hai trường hợp:
3 số đều lẻ
1 số lẻ và 2 số chẵn
Gọi \(B\) là biến cố: “tổng 3 số ghi trên 3 quả cầu là số lẻ”
\(n\left( B \right) = C_{23}^3 + C_{23}^1C_{22}^2 = 7084\)
\(P\left( B \right) = \frac{{7084}}{{14190}} = \frac{{322}}{{645}}\)
d) Đúng. Ta chia các quả cầu thành các nhóm \({C_0};{C_1};{C_2};{C_3}\) là các nhóm chứa các quả cầu lần lượt có các số dư như sau:
\({C_0}\) gồm 11 số chia hết cho 4.
\({C_1}\) gồm 12 số chia hết cho 4 dư 1.
\({C_2}\) gồm 11 số chia hết cho 4 dư 2.
\({C_3}\) gồm 11 số chia hết cho 4 dư 3.
Gọi \(C\) là biến cố: “tổng 3 số ghi trên 3 quả cầu là số chia hết cho 4”.
Xảy ra các trường hợp sau:
Cả 3 số đều thuộc \({C_0}\) có \(C_{11}^3 = 165\) cách chọn.
1 số thuộc \({C_0}\) và 2 số thuộc \({C_2}\) có \(C_{11}^1.C_{11}^2 = 605\) cách chọn.
1 số thuộc \({C_0}\), 1 số thuộc \({C_1}\) và 1 số thuộc \({C_3}\) có \(11 \times 12 \times 11 = 1452\) cách chọn.
1 số thuộc \({C_2}\) và 2 số thuộc \({C_3}\) có \(C_{11}^1.C_{11}^2 = 605\) cách chọn.
2 số thuộc \({C_1}\) và 1 số thuộc \({C_2}\) có \(C_{12}^2.C_{11}^1 = 726\) cách chọn.
\(n\left( C \right) = 3553 \Rightarrow P\left( C \right) = \frac{{3553}}{{C_{45}^3}} = \frac{{323}}{{1290}}\).
Lời giải
Đáp án: 2.
Hàm số \[y = \frac{{{x^2} + (m - 1)x + 3 - 2m}}{{x + m}}\] đạt cực tiểu tại \[x = - 1\] \[ \Leftrightarrow y' = \frac{{{x^2} + 2mx + {m^2} + m - 3}}{{{{\left( {x + m} \right)}^2}}}\] có hai
nghiệm phân biệt \[{x_1},{x_2}\] khác \[ - m\] thoả mãn \[{x_1} = - 1,{x_2} < {x_1}\]
Suy ra \[y'\left( { - 1} \right) = 0 \Rightarrow 1 - 2m + {m^2} + m - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = 2\end{array} \right.\]
Thử lại: Khi \[m = - 1\] thì \[y' = \frac{{{x^2} - 2x - 3}}{{{{\left( {x - 1} \right)}^2}}}\] có hai nghiệm phân biệt \[{x_1} = - 1,{x_2} = 3 > - 1\] (loại).
Khi \[m = 2\] thì \[y' = \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}}\] có hai nghiệm phân biệt \[{x_1} = - 1,{x_2} = - 3 < - 1\] (thoả mãn).
Vậy \[m = 2\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.
\[{\left( {\frac{2}{3}} \right)^{n - 1}}\].
B.
\[{\left( {\frac{2}{3}} \right)^n}\].
C.
\[{\left( {\frac{2}{3}} \right)^{n + 1}}\].
D.
\[{\left( {\frac{2}{3}} \right)^{n + 2}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{1}{3}\).
B. \( - \frac{2}{3}\).
C. 1.
D. 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo