1. Tốt nghiệp THPT
  2. Toán
  3. Đề thi thử Toán THPT Chuyên Bắc Ninh (lần 01) năm 2025-2026 có đáp án

Đề thi thử Toán THPT Chuyên Bắc Ninh (lần 01) năm 2025-2026 có đáp án

48 người thi tuần này 4.6 48 lượt thi 22 câu hỏi

🔥 Đề thi HOT:

2186 người thi tuần này

(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)

33.4 K lượt thi 34 câu hỏi
1241 người thi tuần này

CÂU TRẮC NGHIỆM ĐÚNG SAI

14 K lượt thi 20 câu hỏi
359 người thi tuần này

(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)

6.8 K lượt thi 34 câu hỏi
345 người thi tuần này

Bộ đề thi thử Đại học môn Toán mới nhất cực hay có lời giải (Đề 1)

45.7 K lượt thi 50 câu hỏi
334 người thi tuần này

30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)

158.6 K lượt thi 50 câu hỏi
260 người thi tuần này

20 Bộ đề ôn luyện thi thpt quốc gia môn Toán có lời giải (Đề số 1)

7.6 K lượt thi 50 câu hỏi
247 người thi tuần này

Tổng hợp đề thi thử thptqg môn Toán có lời giải (đề 1)

12.8 K lượt thi 50 câu hỏi
234 người thi tuần này

Các dạng bài tập Cực trị hàm số cực hay có lời giải (P1)

13.7 K lượt thi 22 câu hỏi

Nội dung liên quan:

Đề thi thử Toán THPT chuyên KHTN Hà Nội (lần 01) năm 2025-2026 có đáp án
lượt thi
0 đề

Danh sách câu hỏi:

Câu 1

Cho hàm số \[y = \frac{{2x - 1}}{{x + 1}}\]. Giá trị \[f'\left( 3 \right)\] bằng

A. \[\frac{4}{5}\].

B. \[\frac{3}{{16}}\].

C. \[\frac{2}{9}\].

D. \[\frac{1}{6}\].

Lời giải

Chọn B

Có \[y = \frac{{2x - 1}}{{x + 1}} \Rightarrow y' = \frac{3}{{{{\left( {x + 1} \right)}^2}}} \Rightarrow y'\left( 3 \right) = \frac{3}{{16}}\].

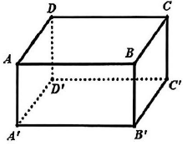
Câu 2

Cho hình lập phương\[ABCD.A'B'C'D'\]. Vectơ nào dưới đây bằng vectơ \[\overrightarrow {AD} \]?
A.

\[\overrightarrow {BC'} \].

B.

\[\overrightarrow {DC} \].

C.

\[\overrightarrow {B'C'} \].

D.

\[\overrightarrow {AB} \].

Lời giải

Chọn C

Câu 3

Tập xác định của hàm số \[y = {\left( {x - 1} \right)^{\frac{1}{6}}} + \log \left( {4 - {x^2}} \right)\] là

A. \[\left[ {1;2} \right)\].

B. \[\left( { - 2;2} \right)\].

C. \[\left( {1;2} \right]\].

D. \[\left( {1;2} \right)\].

Lời giải

Chọn D

Hàm số xác định \[ \Leftrightarrow \left\{ \begin{array}{l}x - 1 > 0\\4 - {x^2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 1\\ - 2 < x < 2\end{array} \right. \Leftrightarrow x \in \left( {1;2} \right)\]

Tập xác định của hàm số \[y = {\left( {x - 1} \right)^{\frac{1}{6}}} + \log \left( {4 - {x^2}} \right)\] là \[D = \left( {1;2} \right)\].

Câu 4

Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm như sau:

Trung vị của mẫu số liệu trên gần với số nào nhất?
A.

\[41,23\].

B.

\[51,54\].

C.

\[40,55\].

D.

\[50,44\].

Lời giải

Chọn B

Tổng số học sinh: \[n = 43\]

Nhóm \[\left[ {40;60} \right]\] là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \[\frac{n}{2} = \frac{{43}}{2} = 21,5\].

Trung vị của mẫu số liệu trên là \[{Q_e} = 40 + \frac{{\frac{{43}}{2} - 14}}{{13}}.20 \approx 51,54\].

Câu 5

Cho hàm số \(y = - {x^3} + 3{x^2} + 9x - 1\). Hệ số góc lớn nhất của tiếp tuyến với đồ thị hàm số là
A.

9.

B.

12.

C.

6.

D.

8.

Lời giải

Chọn B

Hàm số \(y = - {x^3} + 3{x^2} + 9x - 1\)có:

Tập xác định: \(D = \mathbb{R}\)

\(y' = - 3{x^2} + 6x + 9\)

Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ \({x_0}\) là \(k = y'\left( {{x_0}} \right) = - 3{x_0}^2 + 6{x_0} + 9 = - 3{\left( {{x_0} - 1} \right)^2} + 12 \le 12\,,\,\,\forall {x_0} \in \mathbb{R}\)

Vậy hệ số góc lớn nhất của tiếp tuyến với đồ thị hàm số là \(12\), đạt khi \({x_0} = 1\).

Câu 6

Giá trị của giới hạn \({\rm{lim}}\left( {\sqrt[3]{{{n^3} - 2{n^2}}} - n} \right)\) bằng

A. \(\frac{1}{3}\).

B. \( - \frac{2}{3}\).

C. 1.

D. 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

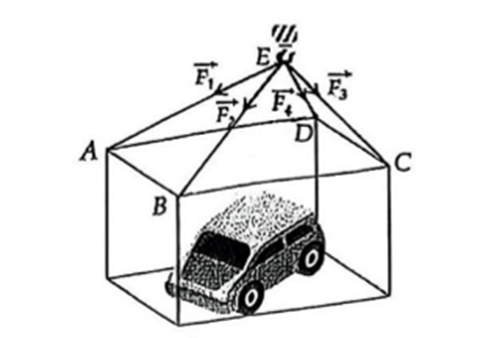
Câu 7

Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng. Gọi \({O_1},{O_2}\) lần lượt là tâm của \(ABCD\,,\,ABEF\). \(M\) là trung điểm của \(CD\). Chọn khẳng định sai trong các khẳng định sau
A.

\(M{O_2}\) cắt \(\left( {BEC} \right)\).

B.

\({O_1}{O_2}\) song song với \(\left( {AFD} \right)\).

C.

\({O_1}{O_2}\) song song với \(\left( {BEC} \right)\).

D.

\({O_1}{O_2}\) song song với \(\left( {EFM} \right)\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Tập giá trị của hàm số \(y = {\rm{cot}}x\) là
A.

\(\left( { - 1;1} \right)\).

B.

\(\left[ { - 1;1} \right]\).

C.

\(\mathbb{R}\).

D.

\(\left( { - \infty ;0} \right)\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

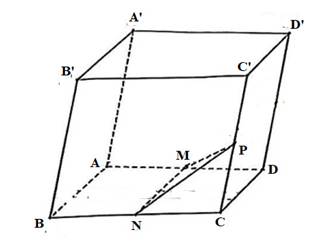
Câu 9

Cho tứ diện \[ABCD\]. Gọi \[G\]là trọng tâm tam giác \[ABC\]. Phát biểu nào sau đây là sai?
A.

\[\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = 3\overrightarrow {DG} \].

B.

\[\overrightarrow {GD} - \overrightarrow {GA} = \overrightarrow {AD} \].

C.

\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \].

D.

\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Cho lăng trụ \[ABCD.A'B'C'D'\]. Có hai đáy là các hình nình hành. Các điểm \[M,N,P\] lần lượt là trung điểm của các cạnh \[AD,\,BC,\,CC'\] (tham khảo hình vẽ). Xét các khẳng định sau:

a) Mặt phẳng \[\left( {MNP} \right)\] cắt \[A'D'\].

b) Mặt phẳng \[\left( {MNP} \right)\] cắt \[DD'\] tại trung điểm của \[DD'\].

c) Mặt phẳng \[\left( {MNP} \right)\] song song với mặt phẳng \[\left( {ABC'D'} \right)\] .

Trong các khẳng định trên, số khẳng định đúng là:

A. 0.        

B. 1.        

C. 3.

D. 2.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Tìm số hạng tổng quát của cấp số nhân lùi vô hạn khi có tổng bằng 3 và công bội bằng \[\frac{2}{3}\].
A.

\[{\left( {\frac{2}{3}} \right)^{n - 1}}\].

B.

\[{\left( {\frac{2}{3}} \right)^n}\].

C.

\[{\left( {\frac{2}{3}} \right)^{n + 1}}\].

D.

\[{\left( {\frac{2}{3}} \right)^{n + 2}}\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Cho hàm số đa thức bậc ba \[y = a{x^3} + b{x^2} + cx + d,\,\,\left( {a \ne 0} \right)\]có đồ thị như hình vẽ.

Cho hàm số đa thức bậc ba y = a{x^3} + b{x^2} + cx + d,(a khác 0) có đồ thị như hình vẽ.Hàm số đã cho nghịch biến trên khoảng nào dưới đây? (ảnh 1)

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

\[\left( { - 2;0} \right)\].

\[\left( {0; + \infty } \right)\].

\[\left( { - 1;1} \right)\].

\[\left( {1; + \infty } \right)\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Cho hàm số y=f(x) có đạo hàm trên ℝ  và f'(x)  là hàm số bậc ba có đồ thị là đường cong trong hình vẽ.

Cho hàm số y=f(x) có đạo hàm trên R và f'(x) là hàm số bậc ba có đồ thị là đường cong trong hình vẽ. (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\), cạnh bên bằng \(\sqrt 2 a\). Gọi \(F\) là trung điểm của cạnh \(SA\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Trong hộp có 45 quả cầu có cùng kích thước và khối lượng được đánh số từ 1 đến 45. Lấy ngẫu nhiên 3 quả cầu từ hộp đó. Xét tính đúng sai của các mệnh đề sau:

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Cho hàm số \[y = {\left( {9 - {x^2}} \right)^{\frac{1}{3}}} + \ln \left( {1 - x} \right)\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) sao cho \(\left| {\overrightarrow a } \right| = \sqrt 2 \), \(\left| {\overrightarrow b } \right| = 2\) và hai vectơ \(\overrightarrow x = \overrightarrow a + \overrightarrow b \), \(\overrightarrow y = 2\overrightarrow a - \overrightarrow b \) vuông góc với nhau. Tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) (đơn vị độ).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Tính tổng tất cả các giá trị nguyên của tham số m để hàm số \[y = \frac{{{x^2} + (m - 1)x + 3 - 2m}}{{x + m}}\] đạt cực tiểu tại \[x = - 1.\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt dạng hình hộp chữ nhật với đáy trên là hình chữ nhật \(ABCD\) , mặt phẳng \(\left( {ABC} \right)\) song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc \(E\) của chiếc cần cẩu sao cho các đoạn dây cáp \(EA;\,EB;\,EC;\,ED\) bằng nhau và cùng tạo với mặt phẳng một góc \(\alpha \).
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt dạng hình hộp chữ nhật với đáy trên là hình chữ nhật ABCD (ảnh 1)
Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết các lực căng \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\,\overrightarrow {{F_3}} ;\,\overrightarrow {{F_4}} \) đều có cường độ là \(4800N\), trọng lượng của cả khung sắt chứa ô tô là \(7200\sqrt 6 N\). Tính \(\sin \alpha \) (Làm tròn kết quả đến chữ số hàng phần trăm).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Cho hình tứ diện \[ABCD\] có tất cả các cạnh bằng \[6.\] Gọi \[M,N\] lần lượt là trung điểm của \[CA,CB.\] \[P\] là điểm trên cạnh \[BD\] sao cho \[BP = 2PD.\] Gọi \[(H)\] là hình giới hạn bởi giao tuyến của mặt phẳng \[(MNP)\] với các mặt của tứ diện \[ABCD.\] Tính diện tích hình \[(H)\] (kết quả làm tròn đến hàng phần trăm).
 

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Mội người đàn ông muốn chèo thuyền ở vị trí \[A\] tới điểm \[B\] về phía hạ lưu bờ đối diện trên một bờ sông thẳng rộng \[3\] km (như hình vẽ). Anh chèo thuyền đến một điểm \[D\] giữa \[C\] và \[B\] và sau đó chạy đến \[B\]. Biết anh ấy có thể chèo thuyền \[6\]km/h, chạy \[8\]km/h và quãng đường \[BC = 8\]km. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến \[B\] là \[a + \frac{b}{c}\sqrt d \] trong đó \[a,b,c,d \in {\mathbb{N}^*}\], \[\frac{b}{c}\] là phân số tối giản và \[d\] là số nguyên tố. Giá trị của \[a + b + c + d\] bằng bao nhiêu?
 
Mội người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện trên một bờ sông thẳng rộng 3 km (ảnh 1)
 
 
 

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Cho hình lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(2\). Hình chiếu vuông góc của \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trọng tâm tam giác \(ABC\). Biết khoảng cách giữa hai đường thẳng \(AA'\) và \[BC\] bằng \(\frac{{\sqrt 3 }}{2}\). Tính thể tích \(V\) của khối lăng trụ \(ABC.A'B'C'\) (kết quả làm tròn đến hàng phần trăm).
 
 
 

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack87. All Rights Reserved.
zalo Nhắn tin Zalo

Đăng ký

Bạn đã có tài khoản?