(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
121 người thi tuần này 4.6 33 K lượt thi 34 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm trường THPT Hà Tĩnh có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Phú Thọ có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Đồng Hỷ (Thái Nguyên) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Trần Phú (Hải Phòng) lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Lê Quý Đôn (Hà Nội) lần 01 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Khuyến (TP.HCM) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Cửa Lò (Nghệ An) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Hạ Long lần 01 có đáp án
Danh sách câu hỏi:
Câu 1
Lời giải
Chọn đáp án B
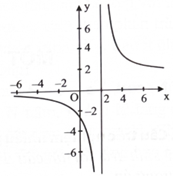
Câu 2
A. xCĐ = -1
Lời giải
Chọn đáp án A
Lời giải
Chọn đáp án C
Câu 4
A. \({\rm{y}} = - 2.\)
Lời giải
Chọn đáp án D
Câu 5
Lời giải
Chọn đáp án C
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. 6,73.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng \(\Delta :\frac{{{\rm{x}} - 2024}}{1} = \frac{{{\rm{y}} - 2025}}{{ - 1}} = \frac{{{\rm{z}} - 2026}}{{\sqrt 2 }}\)
và mặt phẳng \(({\rm{P}}):{\rm{x}} + {\rm{y}} - \sqrt 2 {\rm{z}} - 2025 = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
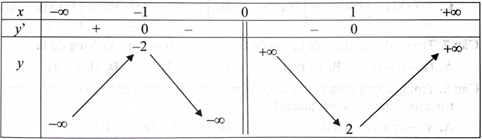
Cho hàm số \({\rm{f}}({\rm{x}}) = {\rm{x}} + \frac{1}{{{\rm{x}} + 2}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Khi kiểm tra thị lực của 240 học sinh khối 12 ở một trường phổ thông, người ta được kết quả như bảng ở hình bên. Chọn ngẫu nhiên 1 học sinh.
|
Thị lực Giới tính |
Nữ |
Nam |
|
Có tật khúc xạ |
47 |
42 |
|
Không có tật khúc xạ |
85 |
66 |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
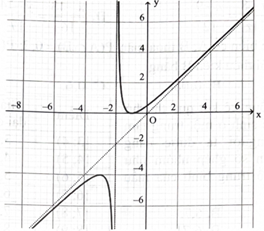
Trong mặt phẳng tọa độ Oxy, xét parabol \(({\rm{P}}):{\rm{y}} = {{\rm{x}}^2} - 4.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
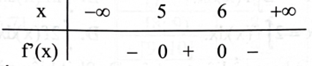
![Cho hàm số \({\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Giá trị lớn nhất của \({\rm{f}}({\rm{x}})\) trên đoạn [1;2] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid2-1727150158.png)