Ôn thi Tốt nghiệp THPT môn Toán (Đề 8)

73 người thi tuần này 4.6 2.3 K lượt thi 51 câu hỏi 90 phút

Đề số 1

🔥 Học sinh cũng đã học

115 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm trường THPT Hà Tĩnh có đáp án

230 lượt thi 12 câu hỏi

71 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Phú Thọ có đáp án

142 lượt thi 22 câu hỏi

72 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Đồng Hỷ (Thái Nguyên) có đáp án

144 lượt thi 22 câu hỏi

56 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Trần Phú (Hải Phòng) lần 1 có đáp án

112 lượt thi 22 câu hỏi

57 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Lê Quý Đôn (Hà Nội) lần 01 có đáp án

114 lượt thi 22 câu hỏi

54 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Khuyến (TP.HCM) có đáp án

108 lượt thi 22 câu hỏi

49 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Cửa Lò (Nghệ An) có đáp án

98 lượt thi 22 câu hỏi

53 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Hạ Long lần 01 có đáp án

106 lượt thi 22 câu hỏi

Danh sách câu hỏi:

Câu 1

Với mọi $n \in N *; k \in N; n ⩾ k$ . Chọn kết luận đúng.

A. $A_{n}^{k} = \frac{n!}{(n - k)!}$

B. $C_{n}^{k} = \frac{n!}{k! (n + k)!}$

C. $A_{n}^{1} = 1$

D. $C_{n}^{0} = 0$

Lời giải

Đáp án đúng là: A

Ta có $A_{n}^{k} = \frac{n!}{(n - k)!}$ ; $C_{n}^{k} = \frac{n!}{k! (n - k)!}$ ; $A_{n}^{1} = n$ ; $C_{n}^{0} = 1$ . Vậy đáp án A đúng.

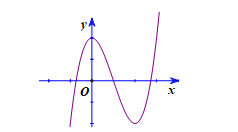
Câu 2

Cho hàm số $y = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình vẽ dưới.

Số điểm cực trị của hàm số đã cho là

A. 2

B. 0

C. 3

D. 1

Lời giải

Đáp án đúng là: A

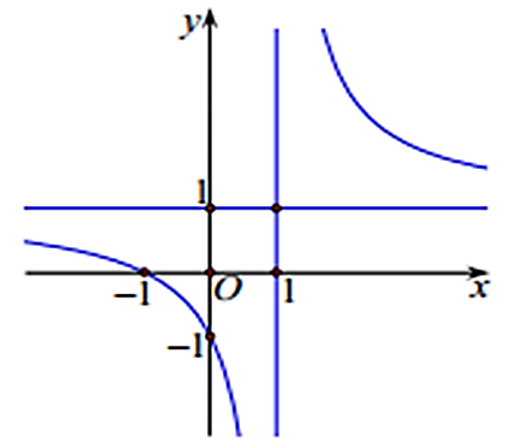
Từ đồ thị đã cho, ta thấy hàm số có 2 cực trị.

Câu 3

Khối đa diện đều loại {3; 5} có số đỉnh, số cạnh và số mặt lần lượt bằng

A. 20; 30; 12

B. 30; 12; 20

C. 12; 30; 20

D. 20; 12; 30

Lời giải

Đáp án đúng là: C

Khối đa diện đều loại {3; 5} là khối hai mươi mặt đều nên có 12 đỉnh, 30 cạnh và 20 mặt.

Câu 4

Giá trị lớn nhất của hàm số $y = x^{3} - 3 x + 1$ trên đoạn $[- 2; 2]$ là

A. 3

B. -2

C. -1

D. 2

Lời giải

Đáp án đúng là: A

Ta có $y = x^{3} - 3 x + 1 \Rightarrow y^{'} = 3 x^{2} - 3$

$y^{'} = 0 \Leftrightarrow x = \pm 1$

$y (- 2) = - 1, y (- 1) = 3, y (1) = - 1, y (2) = 3$

$\Rightarrow \max_{[- 2; 2]} y = 3$ .

Câu 5

Phương trình bậc hai nào sau đây có nghiệm là $1 + 2 i$ ?

A. $z^{2} - 2 z + 5 = 0$

B. $z^{2} + 2 z + 3 = 0$

C. $z^{2} - 2 z + 3 = 0$

D. $z^{2} + 2 z + 5 = 0$

Lời giải

Đáp án đúng là: A

Thử lần lượt từng phương trình ta thấy phương trình ở đáp án A thỏa mãn.

Câu 6

Cho số phức $z = a + b i (a, b \in ℝ)$ . Mệnh đề nào dưới đây sai?

A. $|z| = |\bar{z}| = \sqrt{a^{2} + b^{2}}$

.B. $z \cdot \bar{z}$ là một số thực

z \cdot \bar{z}

là một số thực dương.

z \cdot \bar{z}

là một số phức.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Tập nghiệm của bất phương trình $\log_{\frac{1}{2}} (x + 1) < \log_{\frac{1}{2}} (2 x - 1)$ chứa bao nhiêu số nguyên?

A. 0.

B. 2.

C. Vô số.

D. 1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Tìm nguyên hàm $F (x)$ của hàm số $f (x) = \sin 2 x$ , biết $F (\frac{π}{6}) = 0$ .

A. $F (x) = \sin^{2} x - \frac{1}{4}$

B. $F (x) = {cos}^{2} x - \frac{1}{4}$

C. $F (x) = - \frac{1}{2} cos2 x + \frac{π}{6}$

D. $F (x) = - \frac{1}{2} cos2 x$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Cho hàm số $y = f (x)$ xác định trên $ℝ \ \{1\}$ , liên tục trên các khoảng xác định của nó và có bảng biến thiên như hình vẽ:

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:

A. 0

B. 2

C. 3

D. 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3. Thể tích khối lăng trụ đã cho bằng:

A. $\frac{27 \sqrt{3}}{4}$

B. $\frac{27 \sqrt{3}}{2}$

C. $\frac{9 \sqrt{3}}{4}$

D. $\frac{9 \sqrt{3}}{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Gọi $l, h, R$ lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Đẳng thức nào sau đây luôn đúng?

A. $l^{2} = h R$

B. $R^{2} = h^{2} + l^{2}$

C. $\frac{1}{l^{2}} = \frac{1}{h^{2}} + \frac{1}{R^{2}}$

D. $l^{2} = h^{2} + R^{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Họ tất cả các nguyên hàm của hàm số $f (x) = x^{2}$ là

A. $2 x + C .$

B. $x^{3} + C .$

C. $x + C .$

D. $\frac{x^{3}}{3} + C .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Cho mặt cầu có R là bán kính, S là diện tích mặt cầu và V là thể tích của khối cầu đó. Công thức nào sau đây sai?

A. $S = 4 π R^{2}$

B. $V = \frac{4}{3} π R^{3}$

C. $3 V = S \cdot R$

D. $S = π R^{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Tập nghiệm của phương trình ${(\frac{1}{7})}^{x^{2} - 2 x - 3} = 7^{x + 1}$ là

A. $S = \{- 1; 2\}$

B. $S = \{- 1; 4\}$

C. $S = \{- 1\}$

D. $S = \{2\}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Cho hàm số $y = \frac{2 x + 2}{x - 2}$ . Trong các khẳng định sau, khẳng định nào là đúng?

A. Hàm số đồng biến trên khoảng $(- \infty; 2)$ .

B. Hàm số đồng biến trên khoảng $(2; + \infty)$

C. Hàm số nghịch biến trên $ℝ \ \{2\}$

D. Hàm số nghịch biến trên khoảng $(2; + \infty)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Cho hàm số $y = f (x)$ liên tục trên $ℝ$ và có bảng xét dấu của đạo hàm như hình vẽ.

Hàm số y = f(x) có bao nhiêu điểm cực trị?

A. 4

B. 1

C. 3

D. 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $(P) : 2 x + 2 y - z - 3 = 0$ và điểm $I (1; 2; - 3)$ . Mặt cầu (S) tâm I và tiếp xúc (P) có phương trình:

A. $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 3)}^{2} = 2$

B. $(S) : {(x + 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 4$

C. $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 3)}^{2} = 16$

D. $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 3)}^{2} = 4$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Cho cấp số nhân $(u_{n})$ biết $u_{6} = 2$ và $u_{8} = 8$ . Công bội q của cấp số nhân đã cho bằng

A. $\sqrt{2}$

B. $\pm \frac{1}{2}$

C. 4

D. $\pm 2$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Trong không gian $O x y z$ , gọi đường thẳng $Δ$ là giao tuyến của hai mặt phẳng $(α) : x - 3 y + z = 0$ ; $(β) : x + y - z + 4 = 0$ . Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng $Δ$ ?

A. $\vec{u_{1}} = (4; 2; 2)$

B. $\vec{u_{2}} = (2; 2; 4)$

C. $\vec{u_{4}} = (2; 2; 2)$

D. $\vec{u_{3}} = (2; 4; 2)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Thể tích khối chóp có diện tích đáy B và chiều cao h là

A. $B h$

B. $\frac{1}{3} B h$

C. $\frac{4}{3} B h$

D. $3 B h$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Trong không gian $O x y z$ . Cho mặt phẳng $(P) : x + 3 y - 2 z + 1 = 0$ . Đường thẳng đi qua $A (1; 1; 5)$ và vuông góc với mặt phẳng $(P)$ có phương trình là:

A. $\{\begin{cases} x = 1 + t \\ y = 1 + 4 t \\ z = 5 - 2 t \end{cases}$

B. $\{\begin{cases} x = 1 - t \\ y = 1 - 3 t \\ z = 5 + 2 t \end{cases}$

C. $\{\begin{cases} x = t \\ y = 1 + 3 t \\ z = 5 - 2 t \end{cases}$

D. $\{\begin{cases} x = 1 + t \\ y = 2 + 3 t \\ z = 5 - 2 t \end{cases}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Cho hàm bậc bốn y = f(x) có đồ thị trong hình vẽ bên. Số nghiệm của phương trình $f (x) = \frac{3}{4}$ là:

A. 3

B. 1

C. 2

D. 4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Một hộp chứa 20 thẻ được đánh số từ 1 đến 20. Lẫy ngẫu nhiên 1 thẻ từ hộp đó. Tính xác suất thẻ lấy được ghi số lẻ và chia hết cho 3

A. 0,3

B. 0,25

C. 0,15

C. 0,45

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Cho hàm số $y = f (x)$ xác định và liên tục trên R và có bảng biến thiên như sau:

Mệnh đề nào sau đây là đúng?

A. Hàm số nghịch biến trên khoảng $(1; + \infty)$

B. Hàm số nghịch biến trên khoảng $(- \infty; 1)$

C. Hàm số đồng biến trên khoảng $(- 1; + \infty)$

D. Hàm số đồng biến trên khoảng $(- \infty; - 1)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Cho ba hàm số $y = \log_{a} x; y = \log_{b} x; y = \log_{c} x$ với $a, b, c$ là ba số thực dương, khác 1 có đồ thị như hình vẽ

Khẳng định nào sau đây sai?

A. $0 < a < 1 < c$

B. $0 < a < 1 < b .$

C. $1 < c < b$

D. $b > 1.$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

Đường cong trong hình vẽ dưới là đồ thị của hàm số nào dưới đây?

A. $y = \frac{2 x + 1}{2 x - 1}$

B. $y = \frac{x - 1}{x + 1}$

C. $y = \frac{2 x - 1}{x - 1}$

D. $y = \frac{x + 1}{x - 1}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Đường cong trong hình vẽ dưới là đồ thị của hàm số nào dưới đây?

A. $y = \frac{2 x + 1}{2 x - 1}$

B. $y = \frac{x - 1}{x + 1}$

C. $y = \frac{2 x - 1}{x - 1}$

D. $y = \frac{x + 1}{x - 1}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

Đường cong trong hình vẽ dưới là đồ thị của hàm số nào dưới đây?

A. $y = \frac{2 x + 1}{2 x - 1}$

B. $y = \frac{x - 1}{x + 1}$

C. $y = \frac{2 x - 1}{x - 1}$

D. $y = \frac{x + 1}{x - 1}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

Cho hàm số $f (x)$ liên tục trên R và $\int_{0}^{6} f (x) d x = 12$ . Tính $\int_{0}^{2} f (3 x) d x$ .

A. $\int_{0}^{2} f (3 x) d x = 6$

B. $\int_{0}^{2} f (3 x) d x = 4$

C. $\int_{0}^{2} f (3 x) d x = - 4$

D. $\int_{0}^{2} f (3 x) d x = 36$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Biết $\int_{2}^{3} f (x) d x = 5$ . Khi đó $\int_{2}^{3} [3 - 5 f (x)] d x$ bằng:

A. -15

B. -26

C. -22

D. -28

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

Tập xác định của hàm số $y = {(x - 1)}^{\frac{1}{5}}$ là:

A. $(0; + \infty)$

B. $ℝ$

C. $[1; + \infty)$

D. $(1; + \infty)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

Trong không gian Oxyz, hình chiếu vuông góc của điểm A (1;2;3) trên mặt phẳng (Oyz) là:

A. $N (1; 0; 3) .$

B. $P (1; 0; 0) .$

C. $Q (0; 2; 0) .$

D. $M (0; 2; 3) .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 33

Trong không gian với hệ trục tọa độ $O x y z$ , cho hai vectơ $\vec{u} = (2; 3; - 1)$ và $\vec{v} = (5; - 4; m)$ . Tìm m để $\vec{u} ⊥ \vec{v}$ .

A. $m = - 2.$

B. $m = 2.$

C. $m = 0.$

D. $m = 4.$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 34

Mặt phẳng $(P) : \frac{x}{2} + \frac{y}{3} + \frac{z}{- 2} = 1$ có một vectơ pháp tuyến là:

A. $\vec{n} = (2; 3; 2)$

B. $\vec{n} = (3; 2; - 3)$

C. $\vec{n} = (3; 2; 3)$

D. $\vec{n} = (2; 3; - 2)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 35

Số phức liên hợp của $z = 1 - 2 i$ là

A. $\bar{z} = - 1 - 2 i .$

B. $\bar{z} = - 1 + 2 i .$

C. $\bar{z} = 2 - i .$

D. $\bar{z} = 1 + 2 i .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 36

Số phức $z = a + b i$ , $(a, b \in ℝ)$ có điểm biểu diễn như hình vẽ bên. Tìm a,b .

A. $a = - 4; b = - 3.$

B. $a = 3; b = - 4.$

C. $a = - 4; b = 3.$

D. $a = 3; b = 4.$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 37

Cho đồ thị của hàm số $(C) : y = f (x)$ như hình vẽ. Biết (C) cắt Ox tại 3 điểm có hoành độ lần lượt là $x = - 1; x = 1; x = 2$ và diện tích hình phẳng giới hạn bởi $(C); O x; x = - 1; x = 1$ bằng $S_{1} = 15$ và hai diện tích hình phẳng giới bởi $(C); O x; x = 1; x = 2$ bằng $S_{2} = 3$ .

Giá trị của $\int_{- 1}^{2} f (x) d x$ bằng:

A. 20

B. -10

C. 18

D. 12

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 38

Cho hàm số $y = m x^{4} + (m - 1) x^{2} + 1 - m$ . Tìm tất cả các giá trị của m tham số để hàm số chỉ có một điểm cực trị.

A. $0 \leq m \leq 1$

B. $[_{m > 1}^{m < 0}$

C. 0< m < 1

D. $[_{m \leq 0}^{m \geq 1}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 39

Cho phương trình ${\log_{3}}^{2} (3 x) + \log_{3} (x) + m - 1$ (m là tham số thực). Có bao nhiêu giá trị nguyên của m để phương trình có đúng 2 nghiệm phân biệt thuộc khoảng (0;1)?

A. 1.

B. 0.

C. 2.

D. 3.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 40

Trong không gian, cho vật thể (T) được giới hạn bởi hai mặt phẳng x = -1 và x = 1. Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành x, $(x \in [- 1; 1])$ là một hình vuông có cạnh bằng $2 \sqrt{1 - x^{2}}$ . Thể tích của vật thể (T) bằng:

A. $\frac{16 π}{3}$

B. $π$

C. $\frac{16}{3}$

D. $\frac{8}{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 41

Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a, SA vuông góc với mặt phẳng đáy và SA bằng 2a. Gọi M ,N lần lượt là trung điểm của SA và CD. Khoảng cách giữa hai đường thẳng MN và SC bằng:

A. $\frac{2 a \sqrt{2}}{3}$

B. $\frac{a}{3}$

C. $\frac{a \sqrt{2}}{2}$

D. $\frac{a \sqrt{5}}{6}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 42

Cho số phức z thỏa mãn $(2 - i) z - (2 + i) \bar{z} = 2 i$ . Giá trị nhỏ nhất của $|z|$ bằng:

A. 1.

B. $\frac{\sqrt{5}}{5}$

C. $\frac{2 \sqrt{5}}{5}$

D. 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 43

Một người gửi 100 triệu đồng vào ngân hàng với lãi suất 8,4%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo (lãi kép). Hỏi sau ít nhất n năm $(n \in ℕ^{*})$ thì người đó có được số tiền nhiều hơn 200 triệu đồng.

A. n = 8

B. n = 9

C. n = 10

D. n = 7

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 44

Cho hình trụ có tâm hai đường tròn đáy lần lượt là O và O’, bán kính đáy hình trụ bằng a. Trên đường tròn đáy (O) và (O’) lần lượt lấy hai điểm A, B sao cho AB tạo với trục của hình trụ một góc $30 °$ và có khoảng cách đến trục của hình trụ bằng $\frac{a \sqrt{3}}{2}$ . Tính thể tích khối chop O.O’AB.

A. $\frac{2 π a^{3}}{3}$

B. $\frac{a^{3}}{4}$

C. $\frac{3 a^{3}}{4}$

D. $\frac{\sqrt{3} a^{3}}{4}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 45

Có bao nhiêu giá trị nguyên của tham số $m \in (- 2023; 2023)$ để hàm số $y = |8^{x} - 3 (m + 2) 4^{x} + 3 m (m + 4) 2^{x}|$ đồng biến trên khoảng $(- \infty; 2)$ ?

A. 2022

B. 2020

C. 4039

D. 4037

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 46

Có bao nhiêu cặp số nguyên (x;y) thỏa mãn $0 \leq x \leq 2023$ và $1 \leq y \leq 2023$ và $4^{x + 1} + \log_{2} (y + 3) = 2^{y + 4} + \log_{2} (2 x + 1) .$

A. 2022

B. 1011

C. 4039

D. 4037

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 47

Cho hàm số $y = f (x)$ có đạo hàm liên tục trên $ℝ$ và thỏa mãn $f (x) + f^{'} (x) = 2 x e^{x}$ , $\forall x \in ℝ$ ; $f (\frac{1}{2}) = 0$ . Diện tích hình phẳng giới hạn bởi các đường $y = 2 f (x)$ ; $y = f^{'} (x)$ và trục tung bằng

A. $\frac{2 e \sqrt{e} - 5}{2}$

B. $3 - e$

C. $3 - e^{2}$

D. $\frac{e \sqrt{e} - 5}{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 48

Trong không gian với hệ trục toạ độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} = 8$ và điểm $M (\frac{1}{2}; \frac{\sqrt{3}}{2}; 0)$ . Đường thẳng d thay đổi, đi qua điểm M và cắt mặt cầu (S) tại hai điểm A, B phân biệt. Tính diện tích lớn nhất của tam giác OAB.

A. $2 \sqrt{2}$

B. $2 \sqrt{7}$

C. 4

D. $\sqrt{7}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 49

Cho hình chóp S.ABCD có ABCD là hình thang vuông tại đỉnh A và D. Biết độ dài AB = 4a, AD = 3a, CS = 5a và tam giác SBC đều và góc giữa mặt phẳng (SBC) và (ABCD) bằng $60 ° .$ Tính thể tích khối chóp S.ABCD theo a.

A. $\frac{27 \sqrt{10} a^{3}}{4}$

B. $\frac{27 a^{3}}{4}$

C. $\frac{27 \sqrt{10} a^{3}}{8}$

D. $\frac{27 a^{3}}{8}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 50

Trong không gian với hệ tọa độ $O x y z$ , cho hai đường thẳng $Δ : \frac{x - 3}{1} = \frac{y - 3}{2} = \frac{z - 2}{2}$ và $Δ^{'} : \frac{x - 3}{1} = \frac{y - 3}{- 2} = \frac{z - 2}{2}$ . Mặt phẳng $(P) : 2 x + m y + n z + p = 0$ (m; n; p $\in ℝ$ ) chứa đường thẳng $Δ$ tạo với đường thẳng $Δ'$ một góc lớn nhất. Khi đó tích của m; n; p bằng:

A. 60

B. -30

C. -20

D. 30

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 51

Trên tập hợp số phức, xét phương trình bậc hai $z^{2} - 2 (2 m - 3) z + m^{2} = 0 = 0$ (với m là số thực). Tính tổng tất cả các giá trị của m để phương trình đó có hai nghiệm phân biệt $z_{1}, z_{2}$ thỏa mãn $2 (z_{1} |z_{2}| + z_{2} |z_{1}|) = |z_{1} z_{2}| .$

A. $\frac{12}{7}$

B. $\frac{185}{63}$

C. 0

D. $\frac{11}{9}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tiếng Anh

Công nghệ

Tin học

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Global success

iLearn Smart World

Friends Global

Bright

Explore new worlds

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học