Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Phú Thọ có đáp án

Cho hàm số bậc ba \(y = ax^3 + bx^2 + cx + d\) (a khác 0) có đồ thị như hình vẽ

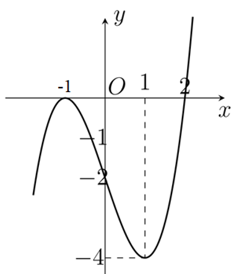
Hàm số nghịch biến trên khoảng nào trong các khoảng dưới đây?

Nghiệm của phương trình \(\sin x = \frac{{\sqrt 3 }}{2}\) là

Cho cấp số nhân \[({u_n})\] có số hạng đầu \[{u_1} = 3\], công bội \[q = - 2\]. Số hạng thứ \[5\]của cấp số nhân đó là

Trong mặt phẳng \[Oxy\], tâm của đường tròn \[\left( C \right):{x^2} + {y^2} + 6x - 4y - 23 = 0\] có tọa độ là

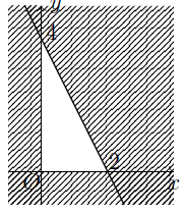
Miền không bị gạch chéo trong hình vẽ (kể cả bờ) là miền nghiệm của hệ bất phương trình nào?

Điểm cực tiểu của hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x - 1\) là

Đường thẳng nào dưới đây là đường tiệm cận xiên của đồ thị hàm số \(y = 2x - 5 + \frac{{10}}{{x + 3}}\)?

Cho hàm số \(y = \frac{{3x + 7}}{{x + 1}}\). Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ {0;3} \right]\) bằng

Trong không gian Oxyz, điểm \[A'\] đối xứng với điểm \[A\left( {2; - 3;1} \right)\] qua mặt phẳng \[\left( {Oxz} \right)\] có tọa độ là

Trong không gian Oxyz, cho \[\overrightarrow a \left( {1;2;3} \right)\] và \[\overrightarrow b \left( {0; - 1;2} \right)\]. Vectơ \[\overrightarrow c = \overrightarrow a - \overrightarrow b \] có tọa độ là

Thời gian truy cập Internet mỗi buổi tối cuả một nhóm học sinh được thống kê trong bảng sau

Khoảng tứ phân vị của mẫu số liệu đã cho bằng:

Cho lăng trụ đều \[ABC.A'B'C'\], có \[AA' = 3a,AB = a\]. Khi đó, côsin của góc giữa hai vectơ \[\overrightarrow {AB'} \] và \[\overrightarrow {A'C} \] bằng

Một cơ sở sản xuất hàng thủ công thống kê về số lượng sản phẩm X bán được trong 30 ngày như sau:

Cho hàm số \(y = {x^3} - 3{x^2} + 5\) có đồ thị là \(\left( C \right)\). Khi đó:

Cho hình chóp đều \(S.ABCD\) có \(SA = AB = 4\sqrt 2 \). Gọi \(M\) là trung điểm của \(AB\), \(G\) là trọng tâm tam giác \(SAB\).

Tại một khu bảo tồn thiên nhiên, các nhà khoa học đã thả một số cá thể của một loài động vật quý hiếm trong một khu rừng rộng 10 hecta và theo dõi sự tăng trưởng số lượng của chúng. Họ thấy rằng số lượng cá thể của loài động vật đó sau \(t\) năm kể từ khi nuôi tại khu bảo tồn được xấp xỉ bởi hàm số \(h\left( t \right) = 70{\log _2}\left( {\frac{{8t + 1}}{{t + 1}}} \right) + 30\) (\(t\) là số thực dương) và tốc độ tăng trưởng số lượng cá thể của loài động vật đó tại thời điểm sau đúng \(t\) năm kể từ khi nuôi được xấp xỉ bởi hàm số \(h'\left( t \right)\)(đơn vị: cá thể /năm).

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật tâm \(O\) với \(AB = 6,AD = 8\). Biết \(SO\) vuông góc với mặt phẳng \((ABCD)\) và \(SA\) tạo với mặt phẳng \((ABCD)\) một góc \({45^\circ }\). Gọi \(M\) là trung điểm của \(SA\). Biết khoảng cách giữa hai đường thẳng \(SC\) và \(DM\) bằng \(\frac{{120}}{{\sqrt n }}\), giá trị của \(n\) bằng bao nhiêu? 

Cho đa giác đều 36 đỉnh \[{A_1}{A_2}...{A_{36}}\] nội tiếp đường tròn tâm \[O\]. Chọn ngẫu nhiên 3 đỉnh trong số các đỉnh \[{A_1},{A_2},...,{A_{36}}\] của đa giác đã cho, biết xác suất để chọn được ba đỉnh tạo thành một tam giác có một góc bằng \[120^\circ \] là \[P\]. Giá trị của biểu thức \[595P\] bằng bao nhiêu?

Cho hình chóp \[S.ABC\], biết \[SA\] vuông góc với mặt phẳng \[\left( {ABC} \right)\] và \[SA = 2\sqrt 3 \]. Tam giác \[ABC\] vuông tại \[B\] với \[AB = 6,BC = 8\]. Gọi \[M\] là trung điểm của \[BC\].

Giá trị của \[\left| {\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  + \overrightarrow {AM} } \right| + \overrightarrow {SM} .\overrightarrow {AB} \] bằng bao nhiêu?

Bác An có một cửa hàng chuyên bán buôn bưởi Đoan Hùng, bác nhận thấy rằng: Nếu bán mỗi kilogram bưởi với giá 30 nghìn đồng thì mỗi tuần có 60 đơn hàng và mỗi đơn hàng mua 100 kilogram. Nếu cứ tăng giá mỗi kilogram bưởi thêm 2 nghìn đồng thì hàng tuần số đơn hàng giảm 4 đơn, đồng thời số lượng bưởi mà mỗi đơn hàng đặt mua cũng giảm đi 2 kilogram. Hỏi bác cần bán mỗi kilogram bưởi với giá bao nhiêu nghìn đồng để lợi nhuận hàng tuần thu được là lớn nhất, biết giá nhập mỗi kilogram bưởi là 24 nghìn đồng và giá bán không vượt quá 50 nghìn đồng/1kg. (Kết quả làm tròn đến hàng đơn vị).