Huyết áp là áp lực của máu tác động lên thành động mạch khi tim bơm máu vào động mạch. Giả sử trong một giai đoạn vận động thể thao, huyết áp của một người thay đổi theo thời gian được cho bởi hàm số \(p\left( t \right) = 100 + 20\cos \left( {120\pi t} \right)\), trong đó \(p\left( t \right)\) là huyết áp tính theo đơn vị mmHg phụ thuộc vào thời gian \(t\) tính theo phút. Trong 10 phút tính từ thời điểm ban đầu khi \(t = 0\), có bao nhiêu lần huyết áp của người này đạt mức 90 mmHg?

Đáp án: \[40\].

Gọi \(x\) là số lần tăng giá (\(x \ge 0\)). Mỗi lần tăng 2 nghìn đồng.

Giá bán mới: \(30 + 2x\) (nghìn đồng). (\(30 + 2x \le 50 \Leftrightarrow x \le 10\))

Tiền lãi trên mỗi kg: \((30 + 2x) - 24 = 6 + 2x\) (nghìn đồng).

Tổng lượng bưởi bán được:

Số đơn hàng: \(60 - 4x\) (đơn).

Số kg mỗi đơn: \(100 - 2x\) (kg).

\( \Rightarrow \) Tổng khối lượng \( = (60 - 4x)(100 - 2x)\).

Hàm lợi nhuận \(L(x)\) thu được là: \(L(x) = (60 - 4x)(100 - 2x)(6 + 2x)\)

\[L(x) = 4(15 - x) \cdot 2(50 - x) \cdot 2(3 + x) = 16 \cdot [(15 - x)(50 - x)(3 + x)] = 16\left( {{x^3} - 62{x^2} + 555x + 2250} \right)\]

\(L'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}{x_1} \approx 36,2(L)\\{x_2} \approx 5,11(N)\end{array} \right.\)

Bảng biến thiên:

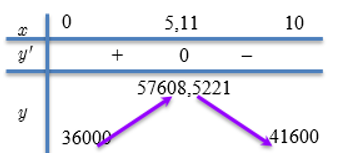
Thay \(x \approx 5,11\) vào công thức giá bán:

\({\rm{Gi\'a b\'a n}} = 30 + 2 \times 5,11 = 40,22{\rm{ }}\)(nghìn đồng)

Làm tròn kết quả đến hàng đơn vị: 40 nghìn đồng.

Đáp án: 1201.

Cách 1:

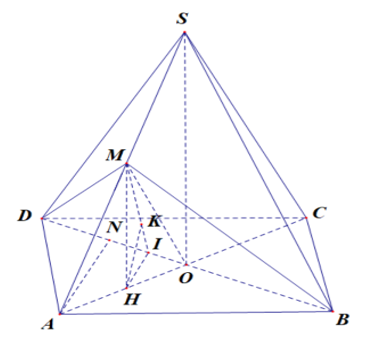
Gọi \(H\) là trung điểm \(AO\). Ta có \(MH\) song song \(SO\) nên \(MH\) vuông góc với \((ABCD)\).

Kẻ \(HI\) vuông góc với \(DB\)\((I \in BD)\), \(HK\) vuông góc với \(MI\) \((K \in MI)\) thì \(HK\) vuông góc với \((MDB)\) nên \(d(H,(MDB) = HK\).

Ta có \(MO\)song song với \(SC\) nên \(d(SC,DM) = d(SC,(MDB)) = d(C,(MDB))\)\( = d(A,(MDB)) = 2.d(H,(MDB)) = 2HK\).

Kẻ \(AN\) vuông góc với \(DB\)\((N \in BD)\), , suy ra \(HI = \frac{1}{2}AN = \frac{{12}}{5}\).

Vì \(SO\) vuông góc với mặt phẳng \((ABCD)\) và \(SA\) tạo với mặt phẳng \((ABCD)\) một góc \({45^\circ }\) nên \(\widehat {SAO} = \)\({45^\circ }\), do đó tam giác \(SAO\) vuông cân tại \(O\), \(SO = AO = \frac{1}{2}BD = 5\), \(HM = \frac{5}{2}\).

Trong tam giác vuông \(HMI\) ta có: \(\frac{1}{{H{K^2}}} = \frac{1}{{H{I^2}}} + \frac{1}{{H{M^2}}} = \frac{{1201}}{{3600}}\)\( \Rightarrow HK = \frac{{60}}{{\sqrt {1201} }}\).

Vậy \(d(DM,SC) = 2.HK = \frac{{120}}{{\sqrt {1201} }}\). Do đó \(n = 1201\).

Cách 2:

1. Xây dựng hệ trục tọa độ và xác định tọa độ các điểm:

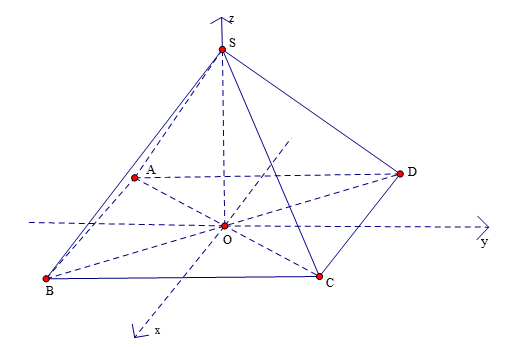
Đặt hệ trục tọa độ \(Oxyz\) sao cho \(O\) là gốc tọa độ \((0,0,0)\).

Vì \(ABCD\) là hình chữ nhật tâm \(O\) với \(AB = 6\) và \(AD = 8\), ta có thể đặt tọa độ các đỉnh của đáy như sau: \(A( - 3, - 4,0)\), \(B(3, - 4,0)\), \(C(3,4,0)\), \(D( - 3,4,0)\).

Kiểm tra lại độ dài các cạnh: \(AB = \sqrt {{{(3 - ( - 3))}^2} + {{( - 4 - ( - 4))}^2} + {{(0 - 0)}^2}} = \sqrt {{6^2}} = 6\);

\(AD = \sqrt {{{( - 3 - ( - 3))}^2} + {{(4 - ( - 4))}^2} + {{(0 - 0)}^2}} = \sqrt {{8^2}} = 8\).
Độ dài đường chéo của hình chữ nhật \(AC = \sqrt {A{B^2} + A{D^2}} = \sqrt {{6^2} + {8^2}} = \sqrt {36 + 64} = \sqrt {100} = 10\).

Vì \(O\) là tâm của hình chữ nhật, \(AO = \frac{1}{2}AC = \frac{1}{2} \cdot 10 = 5\).

Vì \(SO\) vuông góc với mặt phẳng \((ABCD)\), nên \(SO\) là chiều cao của hình chóp và \(S\) nằm trên trục \(Oz\).

Góc giữa \(SA\) và mặt phẳng \((ABCD)\) là góc giữa \(SA\) và hình chiếu của nó lên \((ABCD)\), tức là \(\widehat {SAO}\).

Theo đề bài, \(\widehat {SAO} = {45^\circ }\). Xét tam giác vuông \(SAO\) tại \(O\):

\(SO = AO \cdot \tan (\widehat {SAO}) = 5 \cdot \tan ({45^\circ }) = 5 \cdot 1 = 5\). Vậy tọa độ điểm \(S\) là \((0,0,5)\).

\(M\) là trung điểm của \(SA\). Với \(S(0,0,5)\) và \(A( - 3, - 4,0)\): \(M = \left( { - \frac{3}{2}, - 2,\frac{5}{2}} \right)\).

2. Tính khoảng cách giữa hai đường thẳng \(SC\) và \(DM\):

Đường thẳng \(SC\) đi qua \(S(0,0,5)\) và có vectơ chỉ phương \(\vec u = \overrightarrow {SC} = (3,4, - 5)\).

Đường thẳng \(DM\) đi qua \(D( - 3,4,0)\) và có vectơ chỉ phương \(\vec v = \overrightarrow {DM} = \left( {\frac{3}{2}, - 6,\frac{5}{2}} \right)\).

\(d(SC,DM) = \frac{{\left| {\overrightarrow {SD} .[\vec u,\vec v]} \right|}}{{\left| {\left[ {\vec u,\vec v} \right]} \right|}}\), Vectơ \(\overrightarrow {SD} = ( - 3,4, - 5)\).

Ta có: \(\left[ {\vec u,\vec v} \right] = \)\( = ( - 20, - 15, - 24)\); \(\left| {\overrightarrow {SD} .[\vec u,\vec v]} \right|\)\( = 120\).

\(\left| {\left[ {\vec u,\vec v} \right]} \right| = \sqrt {{{( - 20)}^2} + {{( - 15)}^2} + {{( - 24)}^2}} = \sqrt {400 + 225 + 576} = \sqrt {1201} \).
Khoảng cách giữa hai đường thẳng \(SC\) và \(DM\) là: \(d(SC,DM) = \frac{{|120|}}{{\sqrt {1201} }} = \frac{{120}}{{\sqrt {1201} }}\).

Theo đề bài, khoảng cách này bằng \(\frac{{120}}{{\sqrt n }}\). Do đó, \(\frac{{120}}{{\sqrt n }} = \frac{{120}}{{\sqrt {1201} }}\). Suy ra \(\sqrt n = \sqrt {1201} \).

Vậy \(n = 1201\).