Đề ôn luyện Toán theo Chủ đề 5. Hình học không gian (Đề số 1)
55 người thi tuần này 4.6 0.9 K lượt thi 22 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Trãi (Hà Nội) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Trung Thiên (Hà Tĩnh) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Liên trường THPT Hà Nội lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Thị Minh Khai (Hà Nội) lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Liên trường THPT (Nghệ An) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Đại học Vinh lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm liên trường Nghệ An có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Bắc Ninh có đáp án
Danh sách câu hỏi:
Câu 1
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hình chóp \(S.ABCD\) có đáy \[ABCD\] là hình vuông cạnh \[a\]. Cạnh bên \[SA \bot \,\left( {ABCD} \right),\] \[SA = 2a\]. Khoảng cách từ trung điểm \[M\] của \[AB\] đến mặt phẳng \[\left( {SAD} \right)\] là
Lời giải
Ta có \(MA \bot SA\,\,\left( {{\rm{do}}\,SA \bot \left( {ABCD} \right)} \right)\) và \(MA \bot AD\) nên \[MA \bot \left( {SAD} \right)\] tại \[A\].
Suy ra, khoảng cách từ trung điểm \[M\] của \[AB\] đến \[\left( {SAD} \right)\] là \[MA = \frac{{AB}}{2} = \frac{a}{2}\]. Chọn B.
Câu 2
Lời giải
|
Đặt \(OA = OB = OC = a\). Suy ra \(AB = BC = AC = a\sqrt 2 \). Gọi \(N\) là trung điểm \(AC\) ta có \(MN{\rm{//}}AB\) và \(MN = \frac{{a\sqrt 2 }}{2}\). Suy ra \[\left( {OM,AB} \right) = \left( {OM,MN} \right)\]. Xét tam giác \(OMN\) có \(ON = OM = MN = \frac{{a\sqrt 2 }}{2}\). Do đó, \(\Delta OMN\) là tam giác đều. Suy ra \(\widehat {OMN} = 60^\circ \). |
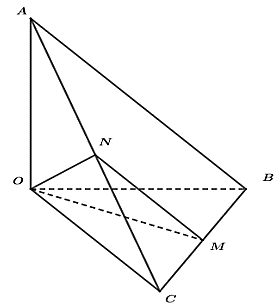 |
Vậy \[\left( {OM,AB} \right) = \left( {OM,MN} \right) = \widehat {OMN} = 60^\circ \]. Chọn C.
Câu 3
Lời giải
Gọi \(O\) là tâm của \(ABCD\) suy ra \(SO \bot \left( {ABCD} \right)\).
Ta có \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{a}{{\sqrt 2 }}\). Chọn A.
Câu 4
Lời giải
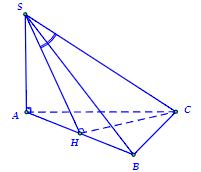
Ta kẻ \(CH \bot AB,\,H \in \,AB\).
\( \Rightarrow \left\{ \begin{array}{l}CH \bot AB\\CH \bot SA\end{array} \right. \Rightarrow CH \bot \left( {SAB} \right)\).
Vậy \(SH\) là hình chiếu vuông góc của đoạn thẳng \(SC\) trên mặt phẳng \(\left( {SAB} \right)\).
Khi đó \(\left( {SC,\left( {SAB} \right)} \right) = \left( {SC,\,SH} \right) = \widehat {CSH}\).
Ta có \[CH = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 \], \(SH = \sqrt {S{A^2} + A{H^2}} = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {a^2}} = a\sqrt 3 \).
Xét tam giác \(SHC\) vuông tại \(H\) ta có: \(\tan \widehat {CSH} = \frac{{CH}}{{SH}} = \frac{{a\sqrt 3 }}{{a\sqrt 3 }} = 1 \Rightarrow \widehat {CSH} = 45^\circ \).
Vậy \(\left( {SC,\,\left( {SAB} \right)} \right) = 45^\circ \). Chọn B.
Câu 5
Lời giải
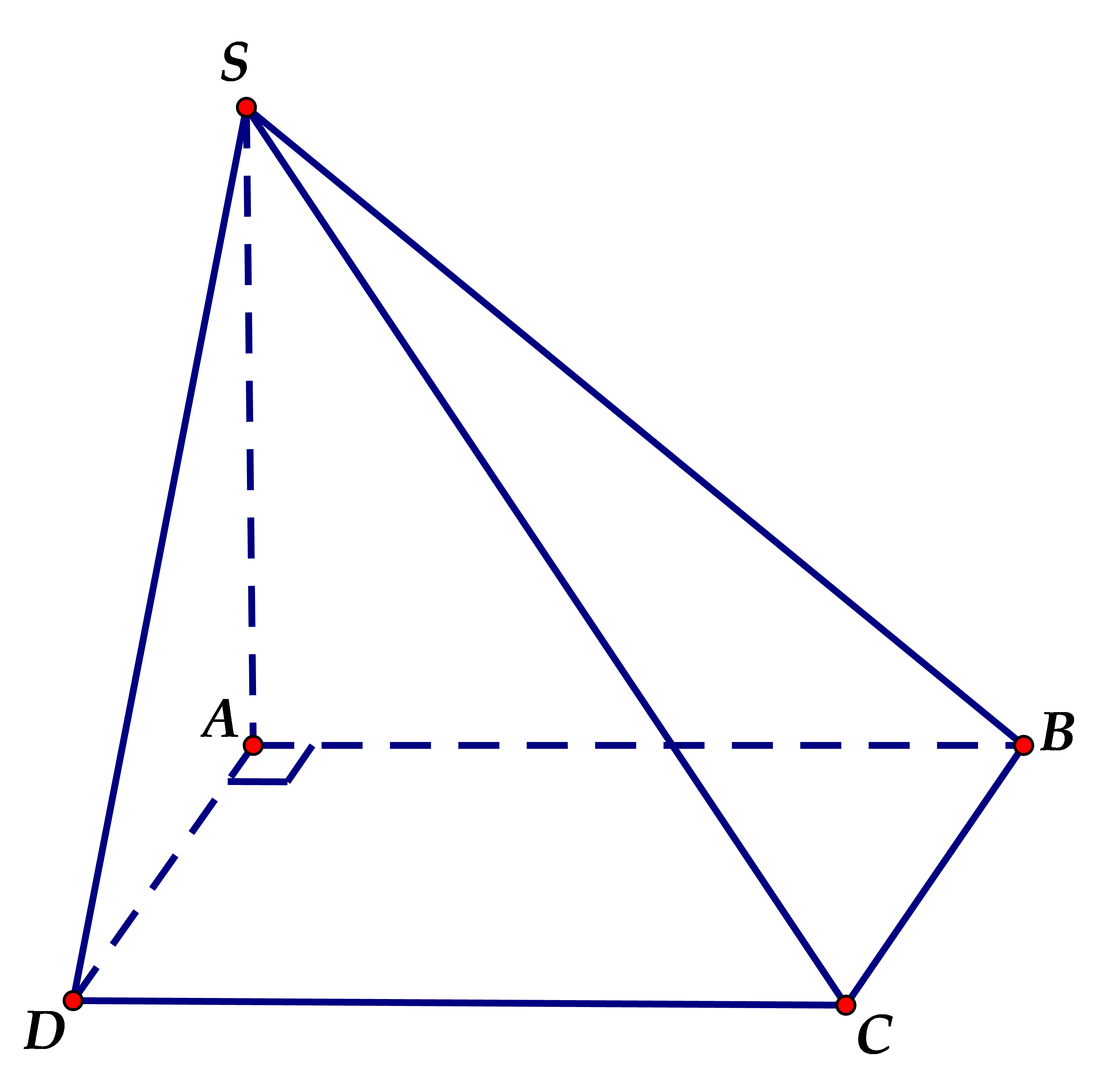
Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AD\).
Ta có \[\left\{ \begin{array}{l}SA \bot AD\\AB \bot AD\end{array} \right. \Rightarrow AD \bot \left( {SAB} \right)\]\[ \Rightarrow d\left( {D,\,\left( {SAB} \right)} \right) = DA\].
Lại có \[\left\{ \begin{array}{l}CD \not\subset \left( {SAB} \right)\\CD\,\,{\rm{//}}\,AB\\AB \subset \left( {SAB} \right)\end{array} \right. \Rightarrow CD\,{\rm{//}}\,\left( {SAB} \right)\].
\[ \Rightarrow d\left( {CD,\,SB} \right)\]\[ = d\left( {CD,\,\left( {SAB} \right)} \right)\]\[ = d\left( {D,\,\left( {SAB} \right)} \right) = DA = a\]. Chọn A.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.