PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh có độ dài bằng \(a\); gọi \(M\), \(N\) lần lượt là trung điểm của \(B'C'\), \(BB'\).
a) Góc giữa hai đường thẳng \(AM\)và \[BC'\] bằng góc giữa hai đường thẳng \(AM\) và \[MN\].
b) Đoạn thẳng \(A'M\) có độ dài bằng \(\frac{{a\sqrt 3 }}{2}\).
c) Đoạn thẳng \(MN\) có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\).
d) Góc giữa hai đường thẳng \(AM\) và \(BC'\) bằng \(60^\circ \).
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh có độ dài bằng \(a\); gọi \(M\), \(N\) lần lượt là trung điểm của \(B'C'\), \(BB'\).
a) Góc giữa hai đường thẳng \(AM\)và \[BC'\] bằng góc giữa hai đường thẳng \(AM\) và \[MN\].
b) Đoạn thẳng \(A'M\) có độ dài bằng \(\frac{{a\sqrt 3 }}{2}\).
c) Đoạn thẳng \(MN\) có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\).
d) Góc giữa hai đường thẳng \(AM\) và \(BC'\) bằng \(60^\circ \).
Quảng cáo
Trả lời:

Ta có, \(MN{\rm{//}}BC'\) nên \(\left( {AM,BC'} \right) = \left( {AM,MN} \right)\).
Xét tam giác \(A'B'M\) vuông tại \(B'\) ta có:
\(A'M\)\( = \sqrt {A'{{B'}^2} + B'{M^2}} \)\( = \sqrt {{a^2} + \frac{{{a^2}}}{4}} \)\( = \frac{{a\sqrt 5 }}{2}\).
Xét tam giác \(AA'M\) vuông tại \(A'\) ta có:
\(AM = \sqrt {A{{A'}^2} + A'{M^2}} \)\( = \sqrt {{a^2} + \frac{{5{a^2}}}{4}} \)\( = \frac{{3a}}{2}\).
Trong \(\Delta AMN\) ta có: \(\cos \widehat {AMN}\)\( = \frac{{M{A^2} + M{N^2} - A{N^2}}}{{2 \cdot MA \cdot MN}}\)\( = \frac{{\frac{{9{a^2}}}{4} + \frac{{2{a^2}}}{4} - \frac{{5{a^2}}}{4}}}{{2 \cdot \frac{{3a}}{2} \cdot \frac{{a\sqrt 2 }}{2}}}\)\( = \frac{{6{a^2}}}{4} \cdot \frac{4}{{6{a^2}\sqrt 2 }}\)\( = \frac{1}{{\sqrt 2 }}\).
Suy ra \(\widehat {AMN} = 45^\circ \). Vậy \(\left( {AM,BC'} \right) = \left( {AM,MN} \right)\)\( = \)\(\widehat {AMN} = 45^\circ \).
Đáp án: a) Đúng, b) Sai, c) Đúng, d) Sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
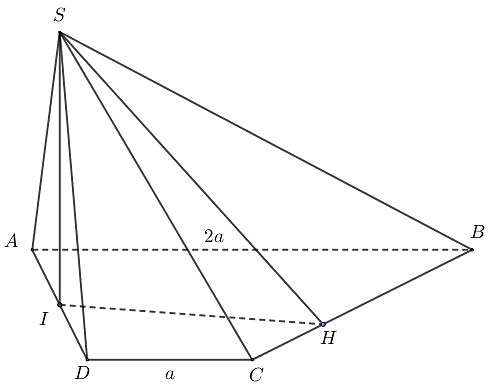
Ta có \(SI\) vuông góc với đáy \(\left( {ABCD} \right)\) và \(BC = \sqrt {{{\left( {2a} \right)}^2} + {a^2}} = a\sqrt 5 \).
Vẽ \[IH \bot CB\] tại \[H\].
Do đó, \(IH\) là hình chiếu của \(SH\) lên mặt phẳng \(\left( {ABCD} \right)\) nên \[SH \bot CB\] (theo định lý ba đường vuông góc).
Khi đó, \[\widehat {SHI}\] là góc phẳng nhị diện của góc nhị diện \(\left[ {S,BC,D} \right]\).
Ta có \[{S_{ICB}} = {S_{ABCD}} - {S_{IDC}} - {S_{AIB}}\]\[ = 3{a^2} - \frac{{{a^2}}}{2} - {a^2} = \frac{{3{a^2}}}{2}\]\[ \Rightarrow IH \cdot CB = 3{a^2}\]\[ \Rightarrow IH = \frac{{3a\sqrt 5 }}{5}\].
Ta có \[\tan \widehat {SHI} = \frac{{SI}}{{IH}}\]\[ = \frac{{\frac{{3a\sqrt 5 }}{5}}}{{\frac{{3a\sqrt 5 }}{5}}} = 1\]\[ \Rightarrow \widehat {SHI} = 45^\circ \].
Đáp án: \[45\].
Lời giải
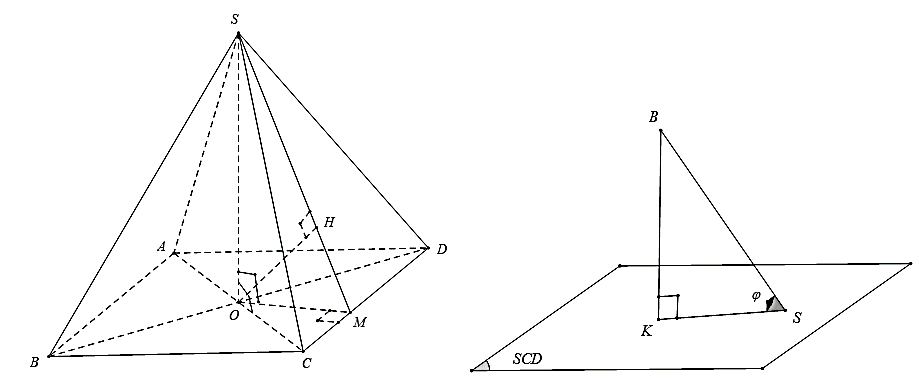
Gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(O,B\) trên mặt phẳng \(\left( {SCD} \right)\).
Khi đó góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {SCD} \right)\) là góc \(\widehat {BSK} = \varphi \).
Ta có \(\sin \varphi = \frac{{BK}}{{BS}}\). Mặt khác \(BK{\rm{//}}\,OH\) và \(\frac{{BK}}{{OH}} = \frac{{BD}}{{OD}} = 2\).
Kẻ \(OM \bot CD\), trong tam giác vuông \(SOM\) có \(\frac{1}{{O{H^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{M^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Ta có \(\Delta SBO = \Delta CBO\) suy ra \(CO = SO = \frac{{a\sqrt 6 }}{3}\) và \(OB = \sqrt {S{B^2} - S{O^2}} = \frac{{a\sqrt 3 }}{3}\).
Þ\(\frac{1}{{O{H^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 6 }}{3}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 6 }}{3}} \right)}^2}}}\) Þ \(OH = \frac{a}{{\sqrt 6 }}\).
Þ\(BK = 2OH = \frac{{2a}}{{\sqrt 6 }}\)Þ\(\sin \varphi = \frac{{\frac{{2a}}{{\sqrt 6 }}}}{a} = \frac{2}{{\sqrt 6 }}\). Suy ra \(\varphi \approx 55^\circ \).
Đáp án: \(55\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.