PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình thang vuông tại \[A\] và \[D\], \[AB = AD = 2a,\] \(CD = a\). Gọi \(I\) là trung điểm cạnh \[AD,\] biết hai mặt phẳng \[\left( {SBI} \right)\], \[\left( {SCI} \right)\] cùng vuông góc với đáy và \[SI = \frac{{3a\sqrt 5 }}{5}\]. Số đo góc nhị diện \(\left[ {S,BC,D} \right]\) bằng bao nhiêu độ?
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình thang vuông tại \[A\] và \[D\], \[AB = AD = 2a,\] \(CD = a\). Gọi \(I\) là trung điểm cạnh \[AD,\] biết hai mặt phẳng \[\left( {SBI} \right)\], \[\left( {SCI} \right)\] cùng vuông góc với đáy và \[SI = \frac{{3a\sqrt 5 }}{5}\]. Số đo góc nhị diện \(\left[ {S,BC,D} \right]\) bằng bao nhiêu độ?
Quảng cáo
Trả lời:
Giải bởi Vietjack
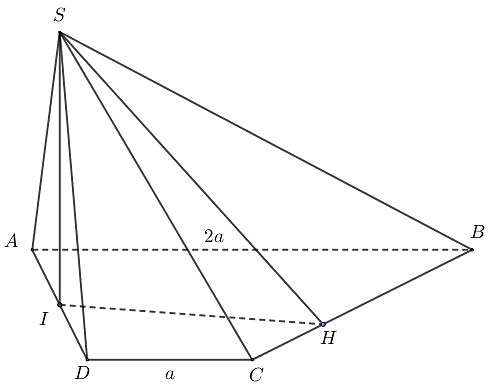
Ta có \(SI\) vuông góc với đáy \(\left( {ABCD} \right)\) và \(BC = \sqrt {{{\left( {2a} \right)}^2} + {a^2}} = a\sqrt 5 \).
Vẽ \[IH \bot CB\] tại \[H\].
Do đó, \(IH\) là hình chiếu của \(SH\) lên mặt phẳng \(\left( {ABCD} \right)\) nên \[SH \bot CB\] (theo định lý ba đường vuông góc).
Khi đó, \[\widehat {SHI}\] là góc phẳng nhị diện của góc nhị diện \(\left[ {S,BC,D} \right]\).
Ta có \[{S_{ICB}} = {S_{ABCD}} - {S_{IDC}} - {S_{AIB}}\]\[ = 3{a^2} - \frac{{{a^2}}}{2} - {a^2} = \frac{{3{a^2}}}{2}\]\[ \Rightarrow IH \cdot CB = 3{a^2}\]\[ \Rightarrow IH = \frac{{3a\sqrt 5 }}{5}\].
Ta có \[\tan \widehat {SHI} = \frac{{SI}}{{IH}}\]\[ = \frac{{\frac{{3a\sqrt 5 }}{5}}}{{\frac{{3a\sqrt 5 }}{5}}} = 1\]\[ \Rightarrow \widehat {SHI} = 45^\circ \].
Đáp án: \[45\].
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
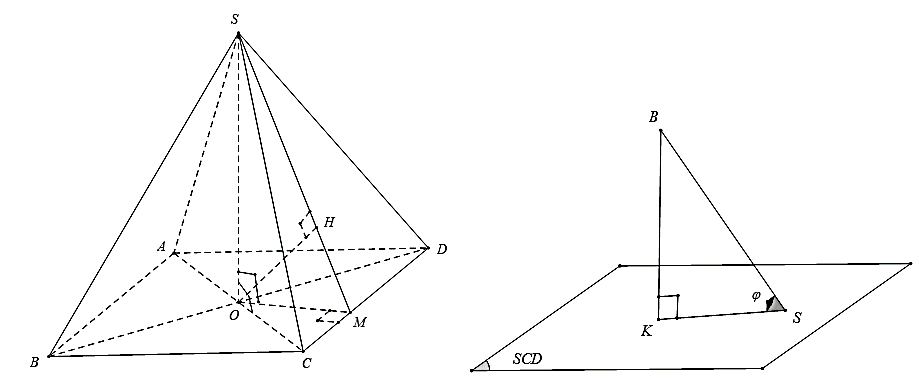
Gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(O,B\) trên mặt phẳng \(\left( {SCD} \right)\).
Khi đó góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {SCD} \right)\) là góc \(\widehat {BSK} = \varphi \).
Ta có \(\sin \varphi = \frac{{BK}}{{BS}}\). Mặt khác \(BK{\rm{//}}\,OH\) và \(\frac{{BK}}{{OH}} = \frac{{BD}}{{OD}} = 2\).
Kẻ \(OM \bot CD\), trong tam giác vuông \(SOM\) có \(\frac{1}{{O{H^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{M^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Ta có \(\Delta SBO = \Delta CBO\) suy ra \(CO = SO = \frac{{a\sqrt 6 }}{3}\) và \(OB = \sqrt {S{B^2} - S{O^2}} = \frac{{a\sqrt 3 }}{3}\).
Þ\(\frac{1}{{O{H^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 6 }}{3}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 6 }}{3}} \right)}^2}}}\) Þ \(OH = \frac{a}{{\sqrt 6 }}\).
Þ\(BK = 2OH = \frac{{2a}}{{\sqrt 6 }}\)Þ\(\sin \varphi = \frac{{\frac{{2a}}{{\sqrt 6 }}}}{a} = \frac{2}{{\sqrt 6 }}\). Suy ra \(\varphi \approx 55^\circ \).
Đáp án: \(55\).
Lời giải
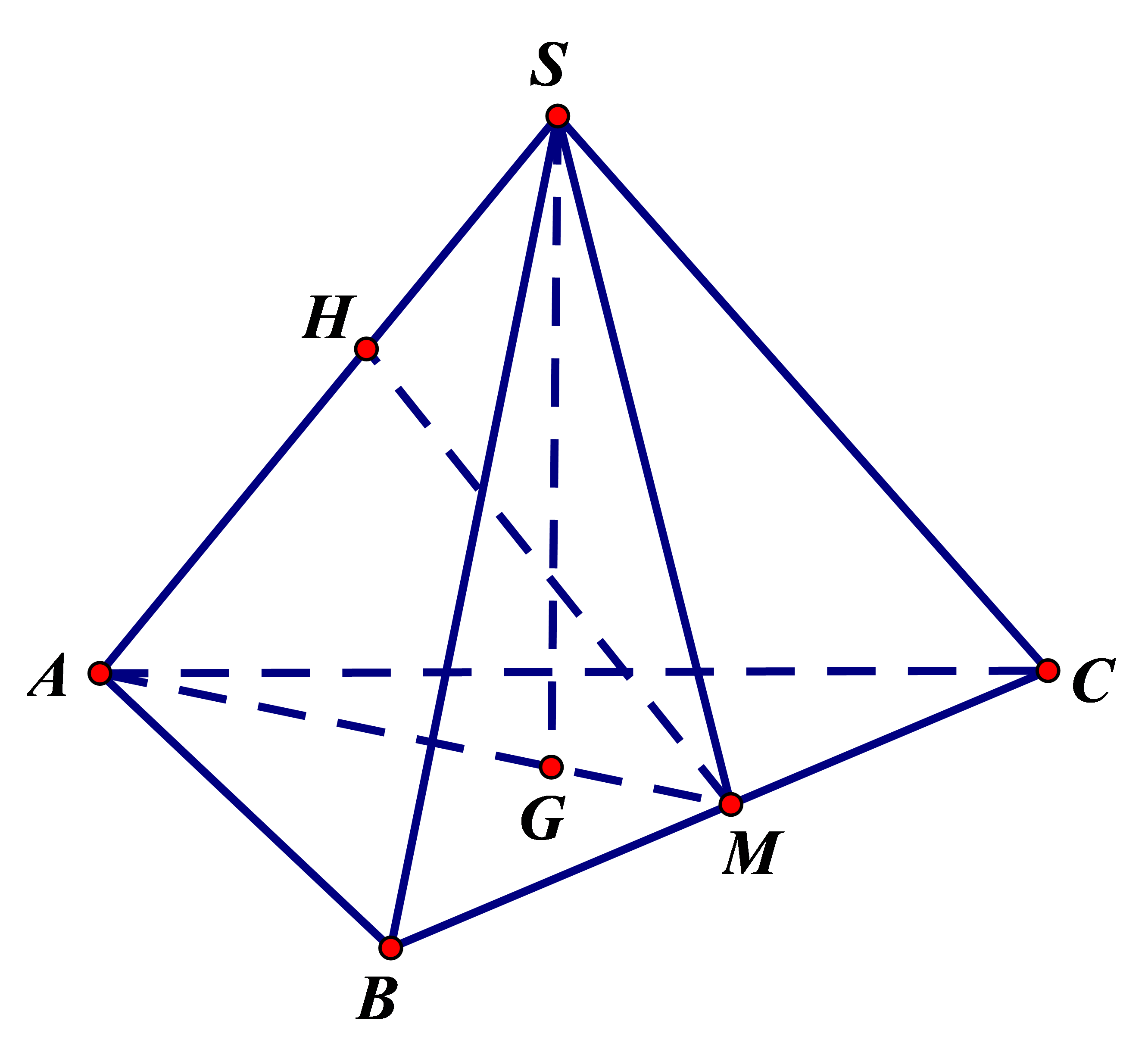
Do hình chóp \[S.ABC\] đều nên \(SG\) là đường cao của hình chóp (\(G\) là trọng tâm tam giác đều \(ABC\)). Kẻ \(MH \bot SA\) tại \(H\) thì \(MH\) là đoạn vuông góc chung của \(SA\) và \(BC\).
Vậy khoảng cách giữa hai đường thẳng \(SA\) và \(BC\) bằng \(MH\).
Do \(\Delta ABC\) đều nên \(AM = \frac{{AB\sqrt 3 }}{2} = \frac{{7\sqrt 3 }}{2}\).
Suy ra \(AG = \frac{2}{3}AM = \frac{{7\sqrt 3 }}{3}\).
Ta có \({V_{S.ABC}} = \frac{1}{3} \cdot \frac{{{7^2}\sqrt 3 }}{4} \cdot SG = \frac{{343\sqrt 3 }}{3}\)\( \Rightarrow SG = 28\).
Lại có \(SA = \sqrt {A{G^2} + S{G^2}} = \frac{{49\sqrt 3 }}{3}\).
Ta có \(\Delta AHM\) đồng dạng với \(\Delta AGS\)\( \Rightarrow \frac{{AM}}{{SA}} = \frac{{MH}}{{SG}} \Rightarrow MH = \frac{{SG \cdot AM}}{{SA}} = \frac{{3 \cdot 28 \cdot 7\sqrt 3 }}{{2 \cdot 49\sqrt 3 }} = 6\).
Đáp án: \(6\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo