Một bể chứa nước hình hộp chữ nhật \(ABCD.A'B'C'D'\) được đặt trên một mái nhà nghiêng so với mặt đất nằm ngang góc \(10^\circ ,\,AB = 1{\rm{\;m}},\,AD = 1,5{\rm{\;m}}\), \(AA' = 1{\rm{\;m}}\). Đáy bể là hình chữ nhật \(ABCD\). Các điểm \(A,B\) cùng ở độ cao \(5{\rm{\;m}}\) (so với mặt đất), các điểm \(C,D\) ở độ cao lớn hơn so với độ cao của các điểm \(A,B\). Khi nước trong bể phẳng lặng người ta đo được khoảng cách giữa đường mép nước ở mặt phẳng \(\left( {ABB'A'} \right)\) và mặt đáy của bể là \(80{\rm{\;cm}}\). Tính thể tích của phần nước trong bể (làm tròn kết quả đến hàng phần trăm theo đơn vị mét khối).
Một bể chứa nước hình hộp chữ nhật \(ABCD.A'B'C'D'\) được đặt trên một mái nhà nghiêng so với mặt đất nằm ngang góc \(10^\circ ,\,AB = 1{\rm{\;m}},\,AD = 1,5{\rm{\;m}}\), \(AA' = 1{\rm{\;m}}\). Đáy bể là hình chữ nhật \(ABCD\). Các điểm \(A,B\) cùng ở độ cao \(5{\rm{\;m}}\) (so với mặt đất), các điểm \(C,D\) ở độ cao lớn hơn so với độ cao của các điểm \(A,B\). Khi nước trong bể phẳng lặng người ta đo được khoảng cách giữa đường mép nước ở mặt phẳng \(\left( {ABB'A'} \right)\) và mặt đáy của bể là \(80{\rm{\;cm}}\). Tính thể tích của phần nước trong bể (làm tròn kết quả đến hàng phần trăm theo đơn vị mét khối).
Câu hỏi trong đề: Đề ôn luyện Toán theo Chủ đề 5. Hình học không gian (Đề số 1) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
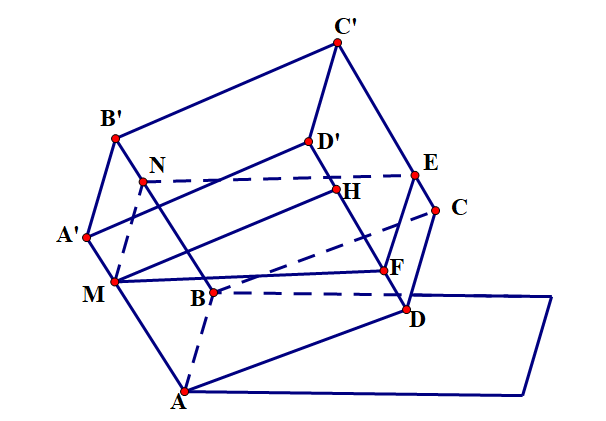
Gọi \(MN\) là đường mép nước ở trên mặt phẳng \(\left( {ABB'A'} \right)\), \(EF\) là đường mép nước trên mặt phẳng \(\left( {CDD'C'} \right)\).
Khi đó \(ABNM.DCEF\) là một hình chóp cụt.
Kẻ \(MH\) vuông góc với \(DD'\) tại \(H\) thì
\(HF = MH \cdot \tan 10^\circ = {\rm{tan}}10^\circ \,\,({\rm{m}})\).
Suy ra \(DF = DH - HF = AM - HF = 0,8 - {\rm{tan}}10^\circ \approx 0,62\,\,({\rm{m}})\).
Ta có \({S_1} = {S_{DCEF}} = DF \cdot CD \approx 0,62\,\,({{\rm{m}}^2});\,\,{S_2} = {S_{ABNM}} = AB \cdot AM = 0,8\,\,({{\rm{m}}^2})\).
Vậy thể tích phần nước trong bể là:
\(V = \frac{1}{3} \cdot \left( {{S_1} + {S_2} + \sqrt {{S_1}{S_2}} } \right) \cdot AD = \frac{1}{3} \cdot \left( {0,62 + 0,8 + \sqrt {0,62 \cdot 0,8} } \right) \approx 0,71\,\,({{\rm{m}}^3})\).
Đáp án: \(0,71\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
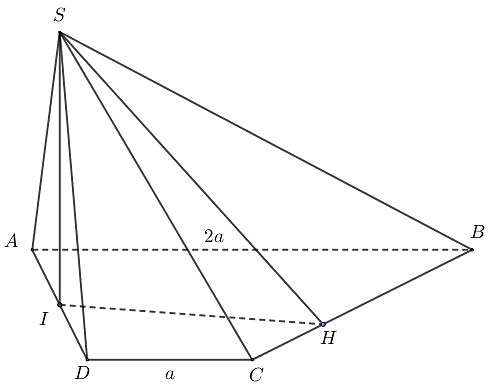
Ta có \(SI\) vuông góc với đáy \(\left( {ABCD} \right)\) và \(BC = \sqrt {{{\left( {2a} \right)}^2} + {a^2}} = a\sqrt 5 \).
Vẽ \[IH \bot CB\] tại \[H\].
Do đó, \(IH\) là hình chiếu của \(SH\) lên mặt phẳng \(\left( {ABCD} \right)\) nên \[SH \bot CB\] (theo định lý ba đường vuông góc).
Khi đó, \[\widehat {SHI}\] là góc phẳng nhị diện của góc nhị diện \(\left[ {S,BC,D} \right]\).
Ta có \[{S_{ICB}} = {S_{ABCD}} - {S_{IDC}} - {S_{AIB}}\]\[ = 3{a^2} - \frac{{{a^2}}}{2} - {a^2} = \frac{{3{a^2}}}{2}\]\[ \Rightarrow IH \cdot CB = 3{a^2}\]\[ \Rightarrow IH = \frac{{3a\sqrt 5 }}{5}\].
Ta có \[\tan \widehat {SHI} = \frac{{SI}}{{IH}}\]\[ = \frac{{\frac{{3a\sqrt 5 }}{5}}}{{\frac{{3a\sqrt 5 }}{5}}} = 1\]\[ \Rightarrow \widehat {SHI} = 45^\circ \].
Đáp án: \[45\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
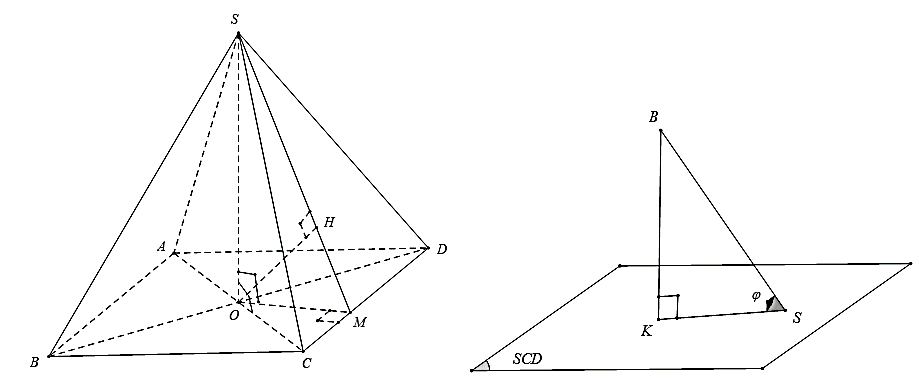
Gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(O,B\) trên mặt phẳng \(\left( {SCD} \right)\).
Khi đó góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {SCD} \right)\) là góc \(\widehat {BSK} = \varphi \).
Ta có \(\sin \varphi = \frac{{BK}}{{BS}}\). Mặt khác \(BK{\rm{//}}\,OH\) và \(\frac{{BK}}{{OH}} = \frac{{BD}}{{OD}} = 2\).
Kẻ \(OM \bot CD\), trong tam giác vuông \(SOM\) có \(\frac{1}{{O{H^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{M^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Ta có \(\Delta SBO = \Delta CBO\) suy ra \(CO = SO = \frac{{a\sqrt 6 }}{3}\) và \(OB = \sqrt {S{B^2} - S{O^2}} = \frac{{a\sqrt 3 }}{3}\).
Þ\(\frac{1}{{O{H^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 6 }}{3}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 6 }}{3}} \right)}^2}}}\) Þ \(OH = \frac{a}{{\sqrt 6 }}\).
Þ\(BK = 2OH = \frac{{2a}}{{\sqrt 6 }}\)Þ\(\sin \varphi = \frac{{\frac{{2a}}{{\sqrt 6 }}}}{a} = \frac{2}{{\sqrt 6 }}\). Suy ra \(\varphi \approx 55^\circ \).
Đáp án: \(55\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập