Ôn thi Tốt nghiệp THPT môn Toán (Đề 16)

39 người thi tuần này 5.0 2.1 K lượt thi 51 câu hỏi 90 phút

Đề số 1

🔥 Học sinh cũng đã học

Đề thi thử Toán Tốt nghiệp Cụm trường QV1-TT1-LVT lần 1 năm 2026 có đáp án

0 lượt thi 22 câu hỏi

Đề thi thử Toán Tốt nghiệp Cụm liên trường Nghệ An lần 1 năm 2026 có đáp án

0 lượt thi 22 câu hỏi

2 người thi tuần này

Đề thi thử Toán Tốt nghiệp THCS - THPT Nguyễn Khuyến - LTT - TPHCM ngày 9-11 có đáp án

4 lượt thi 22 câu hỏi

3 người thi tuần này

Đề thi thử Toán Tốt nghiệp THPT Bãi Cháy lần 01 - Quảng Ninh năm 2025-2026 có đáp án

6 lượt thi 22 câu hỏi

4 người thi tuần này

Đề thi thử Toán Tốt nghiệp THCS - THPT Nguyễn Khuyến - LTT - TPHCM ngày 30-11 có đáp án

8 lượt thi 22 câu hỏi

98 người thi tuần này

Đề thi thử Toán Tốt nghiệp Trường THPT Đào Duy Từ - Thanh Hóa có đáp án

196 lượt thi 22 câu hỏi

68 người thi tuần này

Đề thi thử Toán Tốt nghiệp Trường THPT An Dương - Hải Phòng - Mã đề 001 có đáp án

136 lượt thi 22 câu hỏi

46 người thi tuần này

Đề thi thử Toán Tốt nghiệp Trường THPT An Dương - Hải Phòng - Mã đề 111 có đáp án

92 lượt thi 22 câu hỏi

Danh sách câu hỏi:

Câu 1

Tập nghiệm của bất phương trình $2^{x + 1} \leq 4$ là

A. $(- \infty; 1]$

B. $(1; + \infty)$

C. $[1; + \infty)$

D. $(- \infty; 1)$

Lời giải

Đáp án đúng là: A

Ta có: $2^{x + 1} \leq 4 \Leftrightarrow x + 1 \leq 2 \Leftrightarrow x \leq 1$ .

Vậy phương trình có tập nghiệm $S = (- \infty; 1]$ .

Câu 2

Tích tất cả các nghiệm của phương trình ${log}_{2}^{2} x - 3 {log}_{2} x + 2 = 0$ bằng

A. 8

BB. 6

C. 16

D. 2

Lời giải

Đáp án đúng là: A

Ta có: $\log_{2}^{2} x - 3 \log_{2} x + 2 = 0$ $\Leftrightarrow [\begin{array}{l} \log_{2} x = 1 \\ \log_{2} x = 2 \end{array} \Leftrightarrow [\begin{array}{l} x = 2 \\ x = 4 \end{array}$

Suy ra $x_{1} . x_{2} = 8$ .

Câu 3

Cho $\int \frac{1}{x \ln^{2} x} d x = F (x) + C$ . Khẳng định nào dưới đây đúng?

A. $F^{'} (x) = \frac{- 1}{\ln x}$

B. $F^{'} (x) = \frac{- 1}{\ln x} + C$

C. $F^{'} (x) = \frac{1}{x \ln^{2} x}$

D. $F^{'} (x) = - \frac{1}{\ln^{2} x}$

Lời giải

Đáp án đúng là: C

Vì $\int F^{'} (x) d x = F (x) + C$ . Nên $F^{'} (x) = \frac{1}{x \ln^{2} x}$ .

Câu 4

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng $d : \frac{x - 1}{3} = \frac{y + 2}{- 4} = \frac{z - 3}{- 5}$ . Hỏi d đi qua điểm nào trong các điểm sau:

A. $C (- 3; 4; 5)$

B. $D (3; - 4; - 5)$

C. $B (- 1; 2; - 3)$

D. $A (1; - 2; 3)$

Lời giải

Đáp án đúng là: D

Đường thẳng $d : \frac{x - 1}{3} = \frac{y + 2}{- 4} = \frac{z - 3}{- 5}$ đi qua điểm $A (1; - 2; 3)$ .

Câu 5

Cho khối chóp S.ABC có đáy là tam giác vuông cân tại A, AB = 2, SA vuông góc với đáy và SA = 3 (tham khảo hình bên).

Thể tích khối chóp đã cho bằng

A. 12.

B. 2.

C. 6.

D. 4.

Lời giải

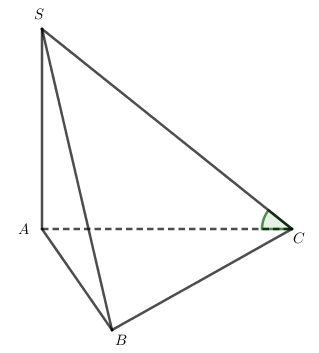
Đáp án đúng là: B

Thể tích khối chóp đã cho bằng $V = \frac{1}{3} B h = \frac{1}{3} . \frac{1}{2} A B . A C . S A = \frac{1}{6} .2.2.3 = 2$ .

Câu 6

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu

$(S) : x^{2} + y^{2} + z^{2} - 2 x + 2 y - 4 z - 2 = 0$ .

Tính bán kính r của mặt cầu.

A. $r = 2 \sqrt[]{2}$

B. $r = \sqrt[]{26}$

C. $r = 4$

D. $r = \sqrt[]{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho một tổ có 15 thành viên. Số cách chọn ra 2 người lần lượt làm tổ trưởng và tổ phó là

A. 225

B. 30

C. 210

D. 105

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Trong không gian Oxyz, cho điểm A (1;2;3). Điểm đối xứng với A qua mặt phẳng (Oyz) có tọa độ là

A. (1;-2;3)

B. (1;2;-3)

C. (-1;-2;-3)

D. (-1;2;3)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Trong không gian Oxyz, mặt phẳng (P): x – 2z + 3 = 0 có một vectơ pháp tuyến là:

A. $\vec{n_{1}} = (1; 0; - 2)$

B. $\vec{n_{4}} = (1; - 2; 3)$

C. $\vec{n_{3}} = (1; - 2; 0)$

D. $\vec{n_{2}} = (- 1; 2; - 3)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Đạo hàm của hàm số $y = π^{x}$ là:

A. $y^{'} = π^{x} \ln π$

B. $y^{'} = x . π^{x - 1}$

C. $y^{'} = \frac{π^{x}}{\ln π}$

D. $y^{'} = \frac{π^{x + 1}}{x + 1}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Trong không gian Oxyz, cho hai điểm M(1;-1;-1) và N(5;5;1). Đường thẳng MN có phương trình là:

A. $\{\begin{cases} x = 5 + 2 t \\ y = 5 + 3 t \\ z = - 1 + t \end{cases}$

B. $\{\begin{cases} x = 5 + t \\ y = 5 + 2 t \\ z = 1 + 3 t \end{cases}$

C. $\{\begin{cases} x = 3 + 2 t \\ y = 2 + 3 t \\ z = t \end{cases}$

D. $\{\begin{cases} x = 1 + 2 t \\ y = - 1 + t \\ z = - 1 + 3 t \end{cases}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Cho hàm số $y = \frac{a x + b}{c x + d}$ có đồ thi là đường cong trong hình bên.

Toạ độ giao điểm của đồ thị hàm số đã cho và trục tung là:

A. (0;-2)

B. (2;0)

C. (-2;0)

D. (0;2)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Cho hàm số y = f(x) xác định và liên tục trên đoạn có [-2;2] và có đồ thị là đường cong trong hình vẽ bên.

Giá trị cực tiểu của hàm số y = f(x) là:

A. -4

B. -2

C. (1;-2)

D. x = 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên.

Có bao nhiêu giá trị nguyên của tham số m để phương trình f(x) = m có ba nghiệm thực phân biệt?

A. 2

B. 5

C. 3

D. 4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Cho hàm số y = f(x) liên tục trên đoạn [a;b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng $x = a; x = b (a < b)$ là:

A. $S = \int_{b}^{a} |f (x)| d x$

B. $S = \int_{a}^{b} f (x) d x$

C. $S = \int_{a}^{b} |f (x)| d x$

D. $S = \int_{b}^{a} f (x) d x$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Trên tập $ℝ \ \{0\}$ , đạo hàm của hàm số $y = {log}_{3} |x|$ là:

A. $y^{'} = \frac{1}{|x| \ln 3}$

B. $y^{'} = \frac{1}{x ln 3}$

C. $y^{'} = \frac{ln 3}{x}$

D. $y^{'} = - \frac{1}{x ln 3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ. Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

A. (-2;2)

B. $(- \infty; 0)$

C. (0;2)

D. $(2; + \infty)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A. $y = \frac{x + 3}{x - 1}$

B. $y = \frac{x - 3}{x - 1}$

C. $y = x^{2} - 4 x + 1$

D. $y = x^{3} - 3 x - 5$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A. $y = \frac{x + 3}{x - 1}$

B. $y = \frac{x - 3}{x - 1}$

C. $y = x^{2} - 4 x + 1$

D. $y = x^{3} - 3 x - 5$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 2 x + 4 y + 6 z + 1 = 0$ . Tâm của (S) có tọa độ là

A. (-1;-2;-3)

B. (2;4;6)

C. (2;3;4)

D. (1;2;3)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Cho hàm số $y = a x^{4} + b x^{2} + c$ có đồ thị là đường cong trong hình bên dưới.

Điểm cực tiểu của hàm số đã cho là

A. $y_{c t} = 1$

B. $x_{c t} = 0$

C. (1;2)

D. (0;1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Cho cấp số nhân $(u_{n})$ với $u_{1} = 2$ và công bội $q = \frac{1}{2}$ . Giá trị của $u_{3}$ bằng

A. 3

B. $\frac{1}{2}$

C. $\frac{1}{4}$

D. $\frac{7}{2} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Cho cấp số nhân $(u_{n})$ với $u_{1} = 2$ và công bội $q = \frac{1}{2}$ . Giá trị của $u_{3}$ bằng

A. 3

B. $\frac{1}{2}$

C. $\frac{1}{4}$

D. $\frac{7}{2} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Cho hình trụ có đường kính đáy 2r và độ dài đường sinh l. Diện tích xung quanh của hình trụ đã cho bằng

A. $2 π r l$

B. $4 π r l$

C. $π r l$

D. $π r^{2} h$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Cho khối lập phương có cạnh bằng 4. Thể tích của khối lập phương đã cho bằng

A.16

B. 8

C. 4

D. 64

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn các số phức z thỏa mãn $|z - 2 i| = 2 023$ là một đường tròn. Tâm của đường tròn đó có tọa độ là

A. (0;2)

B. (-2;0)

C. (0;-2)

D. (2;0)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Tiệm cận đứng của đồ thị hàm số $y = \frac{2 x + 1}{3 x - 1}$ là đường thẳng có phương trình

A. $x = \frac{1}{3}$

B. $y = - \frac{2}{3}$

C. $x = - \frac{1}{3}$

D. $y = \frac{2}{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

Tập nghiệm của bất phương trình $\log (x - 2) < 1$ là

A. $(2; 12)$

B. $(- \infty; 12)$

C. $(- \infty; 3)$

D. $(12; + \infty)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

Giả sử $\int_{0}^{9} f (x) d x = 7$ và $\int_{9}^{0} g (x) d x = 1$ . Khi đó $I = \int_{0}^{9} [2 f (x) + 3 g (x)] d x$ bằng

A. I = 11

B. I = 17

C. I = 23

D. I = 8

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Trên mặt phẳng tọa độ, điểm biểu diễn số phức $z = 7 - 6 i$ có tọa độ là

A. (-6;7)

B. (6;7)

C. (7;6)

D. (7;-6)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

Họ nguyên hàm của hàm số $f (x) = 3 x^{2} + \sin x$ là

A. $x^{3} - \cos x$

B. $6 x + \cos x + C$

C. $x^{3} - \cos x + C$

D. $6 x - \cos x + C$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

Cho hàm số y = f(x) có đạo hàm $f^{'} (x) = {(x - 3)}^{4} (2 - x)$ với mọi $x \in ℝ$ . Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. $(1; 2)$

B. $(3; + \infty)$

C. $(2; + \infty)$

D. $(- \infty; 3)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 33

Trong không gian Oxyz, góc giữa hai mặt phẳng (Oxy) và (Oyz) bằng

A. $30 °$

B. $45 °$

C. $60 °$

D. $90 °$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 34

Với a,b là các số thực dương tùy ý và $a \neq 1$ , $\log_{a^{3}} b$ bằng

A. $3 + \log_{a} b$

B. $3 \log_{a} b$

C. $\frac{1}{3} + \log_{a} b$

D. $\frac{1}{3} \log_{a} b$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 35

Trong hình vẽ bên, điểm M biểu diễn số phức z.

Số phức $\bar{z}$ là

A. $1 - 2 i$

B. $2 + i$

C. $1 + 2 i$

D. $2 - i$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 36

Cho số phức $z = 2 + 9 i$ , phần ảo của số phức $z^{2}$ bằng

A. 36

B. 36i

C. 18

D. 9

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 37

Cho hình chóp S.ABC có $S A ⊥ (A B C)$ ; tam giác ABC đều cạnh a và SA = a. Tìm góc giữa SC và mặt phẳng (ABC).

A. $60 °$

B. $45 °$

C. $90 °$

D. $30 °$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 38

Giải bóng đá Mini cấp trường của một trường THPT, có 16 đội đăng kí tham dự trong đó có 3 đội 12A₁, 12A₂ và 12A₃. Ban tổ chức cho bốc thăm ngẫu nhiên để chia đều 16 đội vào 4 bảng (mỗi bảng 4 đội) để đá vòng loại. Tính xác suất để 3 đội của 3 lớp 12A₁, 12A₂ và 12A₃ nằm ở 3 bảng khác nhau.

A. $\frac{3}{56}$

B. $\frac{19}{28}$

C. $\frac{53}{56}$

D. $\frac{16}{35}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 39

Cho hình chóp S.ABCD, có đáy ABCD là hình vuông cạnh a, $S A ⊥ (A B C D)$ và $S A = \frac{a \sqrt{3}}{3}$ (tham khảo hình bên dưới). Khoảng cách từ điểm A đến mặt phẳng (SCD) là

A. a

B. $\frac{a}{2}$

C. $\frac{a \sqrt{2}}{2}$

D. $\frac{a \sqrt{3}}{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 40

Số các giá trị nguyên của x thỏa $(2^{x^{2}} - 16) (\log_{3} x - 4) \leq 0$ là

A. Vô số

B. 80

C. 17

D. 78

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 41

Gọi $z_{1}, z_{2}$ là hai nghiệm của phương trình $z^{2} - 4 z + 13 = 0$ và A, B lần lượt là hai điểm biểu diễn hai số phức $z_{1}, z_{2}$ trong mặt phẳng Oxy. Diện tích của tam giác OAB bằng

A. 6

B. 12

C. 13

D. $\frac{13}{2} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 42

Cho hàm số y = f(x) có đạo hàm liên tục trên $ℝ$ và thỏa mãn $(x^{3} + 4 x) f^{'} (x) = - (3 x^{2} + 4) f (x) + 4, \forall x \in ℝ$ . Diện tích hình phẳng giới hạn bởi các đường: y = f(x), hai trục tọa độ và x = 2 là

A. Đáp án khác.

B. $\frac{π}{2} .$

C. $\frac{4 π}{3} .$

D. $2 π .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 43

Một cái ly làm bằng thủy tinh, có hình dạng là khối nón cụt và các kích thước như hình vẽ. Phần rỗng bên trong có thiết diện qua trục là Parabol.

Thể tích khối thủy tinh bằng bao nhiêu?

A. $\frac{43}{4} π$

B. $\frac{55}{4} π$

C. $\frac{33}{4} π$

D. $\frac{65}{4} π$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 44

Trong không gian Oxyz, cho điểm A(0;1;2) và đường thẳng $d : \frac{x - 4}{2} = \frac{y - 2}{- 1} = \frac{z - 1}{- 2}$ . Gọi (P) là mặt phẳng chứa d và cách A một khoảng lớn nhất. Khoảng cách từ điểm M(5;-1;3) đến (P) bằng

A. $\frac{2}{3}$

B. $\frac{7}{3}$

C. $\frac{1}{3}$

D. 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 45

Có bao nhiêu giá trị nguyên của tham số $m \in [- 2 023; 2 023]$ để hàm số $y = |\frac{x - 10}{x - m}|$ đồng biến trên khoảng $(- 5; 5] ?$

A. 2017

B. 2019

C. 2018

D. 4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 46

Cho một cổ vật hình trụ có chiều cao đo được là 81 cm, do bị hư hại nên khi tiến hành đo đạc lại thu được AB = 50 cm, BC = 70 cm, CA = 80 cm, với A, B, Cthuộc đường tròn nắp trên như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nào sau đây?

A. $6,56 m^{3}$

B. $0,42 m^{3}$

C. $1,03 m^{3}$

D. $0,43 m^{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 47

Cho tứ diện ABCD có AB = a, $A C = a \sqrt{5}$ , $\hat{D A B} = \hat{C B D} = 90 °$ , $\hat{A B C} = 135 °$ . Biết góc giữa hai mặt phẳng (ABD) và (BCD) bằng $30 °$ . Thể tích khối tứ diện ABCD bằng

A. $\frac{a^{3}}{\sqrt{2}}$

B. $\frac{a^{3}}{3 \sqrt{2}}$

C. $\frac{a^{3}}{2 \sqrt{3}}$

D. $\frac{a^{3}}{6}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 48

Trong không gian Oxyz, cho hai điểm A(0;0;10) và $B (3; 4; \frac{19}{2})$ . Xét các điểm M thay đổi sao cho tam giác OAM không phải là tam giác nhọn và có diện tích bằng 20. Giá trị nhỏ nhất của độ dài đoạn thẳng MB thuộc khoảng nào dưới đây?

A. (5;10)

B. (3;5)

C. $(\frac{3}{2}; 3)$

D. $(0; \frac{3}{2})$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 49

Cho các số phức z, w, u thỏa mãn $|z - 4 + 2 i| = |2 z + \bar{z}|$ , $\frac{w - 8 - 10 i}{w - 6 - 10 i}$ là số thuần ảo và \ $|u + 1 - 2 i| = |u - 2 + i|$ . Giá trị nhỏ nhất của $P = |u - z| + |\bar{u} - \bar{w}|$ thuộc khoảng nào sau đây?

A. (0;5]

B. (5;8)

C. [8;10)

D. $[10; + \infty)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 50

Có bao nhiêu số nguyên dương y để tồn tại số thực x > 1 thỏa mãn

$x (2^{x y} + \log_{2} (x y)) = x y^{4} + 15 x y - 30 + 10 y$ ?

A. 16

B. 15

C. 26

D. 27

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 51

Cho hàm số $f (x) = {(x - 3)}^{2} {(2 x - 7)}^{3} {(3 x - 10)}^{2 023} {(x - 4)}^{2 024}$ . Biết rằng tập hợp tất cả các giá trị thực của tham số m để hàm số $h (x) = f (|- x^{4} + 8 x^{2} + m x|)$ có số điểm cực tiểu nhiều nhất là $S = (a; b) \ \{c\}$ . Giá trị của biểu thức $T = a^{2} - a b + b^{2} + a b c$ thuộc khoảng nào sau đây?

A. (1;100)

B. (115;130)

C. (100;115)

D. (130;2023)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Bright

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý