Có bao nhiêu số nguyên dương y để tồn tại số thực x > 1 thỏa mãn
?
Có bao nhiêu số nguyên dương y để tồn tại số thực x > 1 thỏa mãn
?
A. 16
B. 15
C. 26
D. 27
Câu hỏi trong đề: Ôn thi Tốt nghiệp THPT môn Toán (Đề 16) !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
Đầu tiên ta có phương trình sau: (*)
(1)
Giải thích: ta cô lập vế phải là một hàm theo biến y luôn đồng biến trên ( ).
Tiếp theo ta khảo sát hàm số trên .
Ta có:.
Thế vào ta có .
Suy ra thì , kéo theo đó ta có được:
.
Khi ấy để (*)có nghiệm thì cần có:
(2)
Từ (1) và (2) ta suy ra
(3)
Cho vế trái (3) bằng không giải ra nghiệm (shift SOLVE) (**), khi đó ta có ý tưởng sau:
Giả sử đảo chiều (3), ta có:
(4).
Tới đây ta sẽ chứng minh bất phương trình (4) luôn đúng với mọi .
Xét hàm số có nên suy ra tức .
Suy ra bất phương trình (4) luôn đúng với mọi tức bất phương trình (3) luôn đúng với mọi .
Do (**) nên ta thử từng giá trị theo thứ tự từ lớn xuống.
Nhận thấy y = 17 không thỏa nên
Mà đề cho nên ta thử hai giá trị còn lại lần lượt là , nhận thấy hai giá trị này đều thỏa nên suy ra tức . Vậy có tất cả 16 giá trị nguyên y thỏa mãn đề bài.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
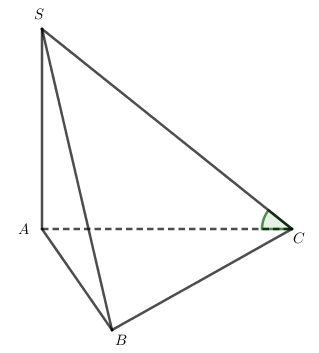
Kẻ tại H.
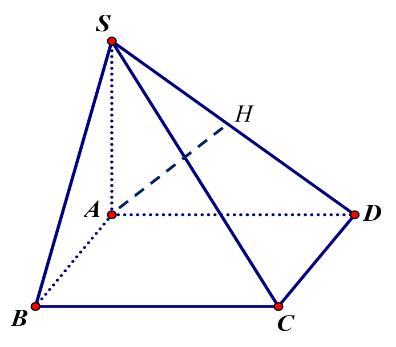
Dễ thấy .
Mà Þ .
Suy ra .
Áp dụng hệ thức lượng trong có:
.
Vậy .
Lời giải
Đáp án đúng là: B
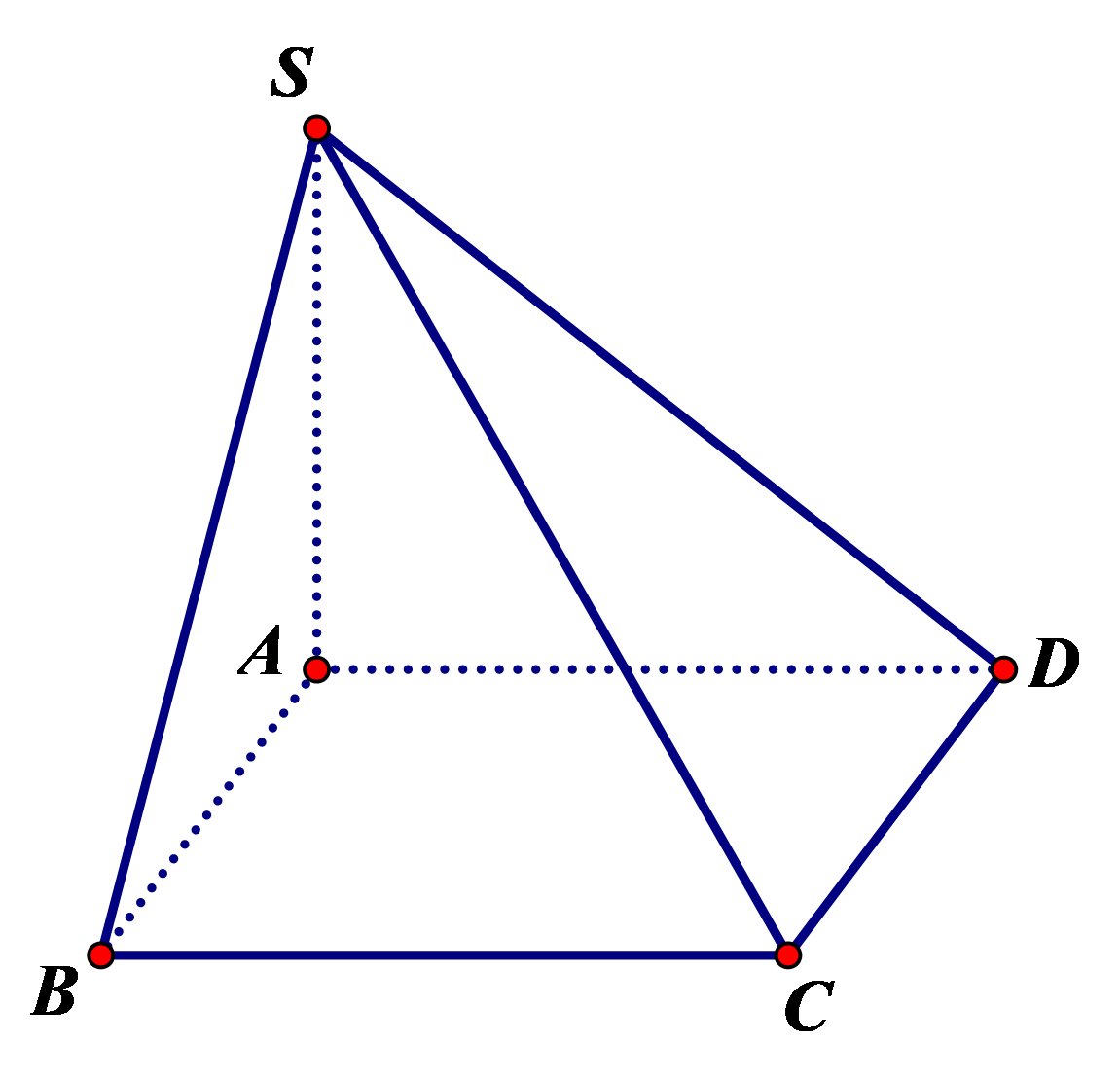
Vì nên AC là hình chiếu của AC trên mặt phẳng (ABC).
Khi đó, góc giữa SC và mặt phẳng (ABC) là (do vuông cân tại A cạnh a).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
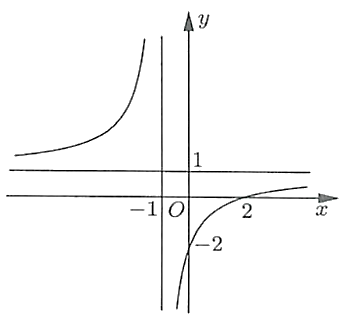
Câu 4
A. (0;2)
B. (-2;0)
C. (0;-2)
D. (2;0)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. (0;-2)
B. (2;0)
C. (-2;0)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.