Một công ty thực phẩm muốn tạo ra một loại thức ăn hỗn hợp cho vật nuôi từ hai nguyên liệu chính là ngô và đậu nành. Biết rằng 1 kg ngô có \(0,1{\rm{\;kg}}\) protein và \(0,6{\rm{\;kg}}\) carbohydrate, 1 kg đậu nành có \(0,4{\rm{\;kg}}\) protein và \(0,3{\rm{\;kg}}\) carbohydrate. Công ty cần sản xuất một bao thức ăn hỗn hợp sao cho tổng khối lượng ngô và đậu lành không vượt quá 100 kg và phải đảm bảo chứa ít nhất 20 kg protein và ít nhất \(46,5{\rm{\;kg}}\) carbohydrate. Giá thành mỗi kg ngô là 5 nghìn đồng và mỗi kg đậu nành là 9 nghìn đồng. Hỏi chi phí sản xuất một bao thức ăn của công ty thấp nhất là bao nhiêu nghìn đồng?

Ta có đạo hàm

\(C'\left( t \right) = \frac{{120\left( {{t^2} + 36 - 2{t^2}} \right)}}{{{{\left( {{t^2} + 36} \right)}^2}}} = \frac{{120\left( {36 - {t^2}} \right)}}{{{{\left( {{t^2} + 36} \right)}^2}}}\)

\(C'\left( t \right) = 0 \Leftrightarrow 36 - {t^2} = 0 \Leftrightarrow \left[ \begin{array}{l}t = 6\\t = - 6\end{array} \right.\).

Ta có bảng biến thiên

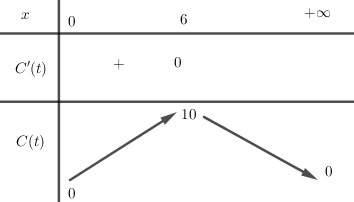
Vì vậy nồng độ thuốc tối đa là \({\rm{10mg/L}}\).

Đáp án: 63.

Xét điểm \[{\rm{K}}\]:

\[2M{A^2} + M{B^2} = 2{\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} = 2{\left( {\overrightarrow {MK} + \overrightarrow {KA} } \right)^2} + {\left( {\overrightarrow {MK} + \overrightarrow {KB} } \right)^2} = 3M{K^2} + 2K{A^2} + K{B^2} + \overrightarrow {MK} .\left( {2\overrightarrow {KA} + \overrightarrow {KB} } \right)\]

Chọn điểm \[{\rm{K}}\] thoả mãn \[2\overrightarrow {KA} + \overrightarrow {KB} = \overrightarrow 0 \] , gọi \[{\rm{K}}\left( {{\rm{x;y;z}}} \right)\]. Khi đó

\[\left\{ \begin{array}{l}2\left( {2 - x} \right) + \left( { - 1 - x} \right) = 0\\2\left( {0 - y} \right) + \left( { - 6 - y} \right) = 0\\2\left( {1 - z} \right) + \left( {7 - z} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 2\\z = 3\end{array} \right. \Rightarrow K\left( {1; - 2;3} \right)\]

Khi đó\[2M{A^2} + M{B^2} = 3M{K^2} + 2K{A^2} + K{B^2}\] nhỏ nhất khi \[{\rm{M}}\] là hình chiếu của \[{\rm{K}}\] trên mặt phẳng \[\left( P \right)\]. \[{\rm{MK = d}}\left( {{\rm{K,}}\left( P \right)} \right) = \sqrt 3 \].,\[{\rm{M}}{{\rm{K}}^{\rm{2}}}{\rm{ = 3, K}}{{\rm{A}}^{\rm{2}}} = 9,{\rm{K}}{{\rm{B}}^{\rm{2}}} = 36.\] Suy ra giá trị nhỏ nhất cần tìm là \[{\rm{63}}\].