Một công ty sau khi ra mắt sản phẩm mới đã ghi nhận lợi nhuận \(P\left( t \right)\) (đơn vị: tỷ đồng) sau \(t\) tháng kinh doanh. Trong năm đầu tiên, giả sử mối liên hệ giữa lợi nhuận và thời gian kinh doanh được mô hình hóa bởi hàm số:
\(P\left( t \right) = - {t^3} + 12{t^2} + 60t - 50\), \(0 \le t \le 12\).
Quảng cáo
Trả lời:
a) Đúng.
Lợi nhuận của công ty tại thời điểm \(t = 2\): \(P\left( 2 \right) = - {2^3} + 12 \times {2^2} + 60 \times 2 - 50 = 110\) tỷ đồng.
b) Sai.
Hàm số biểu thị tốc độ tăng trưởng lợi nhuận: \(P'\left( t \right) = - 3{t^2} + 24t + 60\).
c) Đúng.
Hàm số \(P\left( t \right)\) liên tục trên đoạn \(\left[ {0;12} \right]\).
Ta có: \[P'\left( t \right) = - 3{t^2} + 24t + 60 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 10 \in \left[ {0;12} \right]\\t = - 2 \notin \left[ {0;12} \right]\end{array} \right.\].
Xét trên đoạn \(\left[ {0;12} \right]\):
+ \(P\left( 0 \right) = - {0^3} + 12 \times {0^2} + 60 \times 0 - 50 = - 50\);
+ \(P\left( {10} \right) = - {10^3} + 12 \times {10^2} + 60 \times 10 - 50 = 750\);
+ \(P\left( {12} \right) = - {12^3} + 12 \times {12^2} + 60 \times 12 - 50 = 670\).
Vậy lợi nhuận của công ty đạt mức tối đa là \({P_{\max }} = 750\) tỷ đồng tại thời điểm \(t = 10\).
d) Đúng.
Ta có: \(P'\left( t \right) = - 3{t^2} + 24t + 60 = - 3\left( {{t^2} - 8t + 16} \right) + 108 = - 3{\left( {t - 4} \right)^2} + 108 \le 108\).
Dấu bằng xảy ra khi \( - 3{\left( {t - 4} \right)^2} = 0 \Leftrightarrow t = 4\).
Vậy tốc độ tăng trưởng lợi nhuận là lớn nhất tại thời điểm \(t = 4\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x,y\) lần lượt là số kg cần thiết để sản xuất một bao sản phẩm thức ăn hỗn hợp, \(x,y \ge 0\).
Ta có hệ điều kiện
\(\left\{ \begin{array}{l}0,1.x + 0,4.y \ge 20\\0,6.x + 0,3.y \ge 46,5\\x + y \le 100\end{array} \right.\)
Hàm mục tiêu \(T = 5x + 9y\).
\(\begin{array}{l}\left( {{d_1}} \right):0,1.x + 0,4.y = 20\\\left( {{d_2}} \right):0,6.x + 0,3.y = 46,5\\\left( {{d_3}} \right):x + y = 100\end{array}\)
Các giao điểm \(A\left( {60;35} \right),B\left( {\frac{{20}}{3};\frac{{100}}{3}} \right),C\left( {55;45} \right)\)
Gía trị hàm mục tiêu tại các đỉnh \(T\left( A \right) = 615;T\left( B \right) = \frac{{1900}}{3},T\left( C \right) = 680\). Vậy chi phí thấp nhất là 615(nghìn đồng)
Lời giải
Ta có đạo hàm
\(C'\left( t \right) = \frac{{120\left( {{t^2} + 36 - 2{t^2}} \right)}}{{{{\left( {{t^2} + 36} \right)}^2}}} = \frac{{120\left( {36 - {t^2}} \right)}}{{{{\left( {{t^2} + 36} \right)}^2}}}\)
\(C'\left( t \right) = 0 \Leftrightarrow 36 - {t^2} = 0 \Leftrightarrow \left[ \begin{array}{l}t = 6\\t = - 6\end{array} \right.\).
Ta có bảng biến thiên
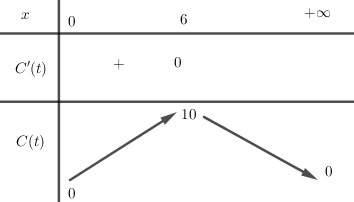
Vì vậy nồng độ thuốc tối đa là \({\rm{10mg/L}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.