1. Thực hiện phép tính (tính nhanh nếu có thể):
(a) \[143\,\,.\,\,126 - 143\,\,.\,\,26\]
(b) \[3\,\,.\,\,{2^6}\,\,.\,\,125\].
2. Tìm \[x\], biết:
(a) \(5\left( {x + 1} \right) = 35\)
(b) \[2x - 138{\rm{ }} = {2^3}\,\,.\,\,{3^2}.\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
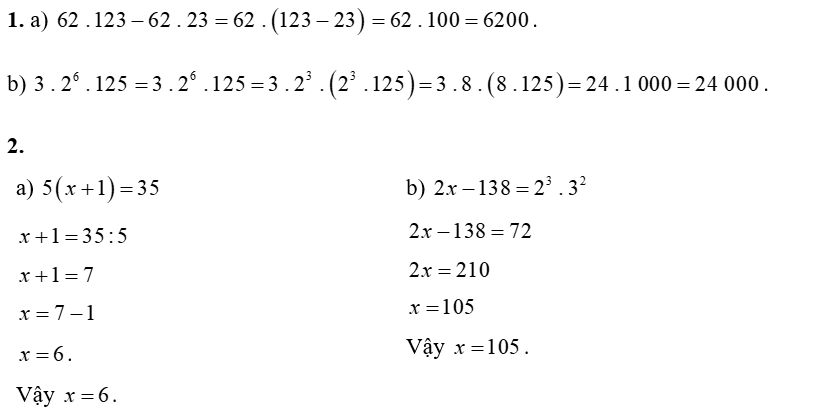
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(a\) (học sinh) là số học sinh khối \(6\) và \(7\) của trường đó (\(250 < a < 300\)).
Số học sinh khối \(6\) và \(7\) là bội chung của \(8\); \(10\) và \(12\).
Ta có: \(8 = {2^3}\); \(10 = 2\,.\,\,5\); \[12 = {2^2}\,.\,3\].
\({\rm{BCNN}}\left( {8,\,\,10,\,\,12} \right) = 120\) nên \({\rm{BC}}\left( {8,\,\,10,\,\,12} \right) = \left\{ {0;\,\,120;\,\,240;\,\,360;...} \right\}\).
Vì số học sinh khối \(6\) và \(7\) của một trường khoảng từ \(250\) đến \(300\) em nên số học sinh của trường đó là \(240\) học sinh.
Lời giải
Ta có \[A = 2 + {2^2} + {2^3} + \ldots + {2^{20}}\]
\[ = (2 + {2^2}\; + {2^3} + {2^4}) + ({2^5} + {2^6}\; + {2^7} + {2^8}) + \ldots + ({2^{17}} + {2^{18}}\; + {2^{19}} + {2^{20}})\]
\[ = 2(1 + 2 + {2^2} + {2^3}) + {2^5}(1 + 2 + {2^2} + {2^3}) + \ldots + {2^{17}}(1 + 2 + {2^2} + {2^3})\]
\[ = (1 + 2 + {2^2} + {2^3})(2 + {2^5} + \ldots + {2^{17}})\]\[ = 25(2 + {2^5} + \ldots + {2^{17}})\].
Vì \(25\,\, \vdots \,\,5\) nên \[25(2 + {2^5} + \ldots + {2^{17}})\,\, \vdots \,\,5\].
Vậy biểu thức A chia hết cho 5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\[\left( {a + b + c} \right)\,\, \vdots \,\,3\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,6\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,9\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,27\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo