Trong các dãy số sau, dãy số nào là một cấp số nhân?

a) \[\lim \frac{{{{4.3}^n} + {7^{n + 1}}}}{{{{2.5}^n} + {7^n}}} = \lim \frac{{{{4.3}^n} + {{7.7}^n}}}{{{{2.5}^n} + {7^n}}} = \lim \frac{{4.{{\left( {\frac{3}{7}} \right)}^n} + 7}}{{2.{{\left( {\frac{5}{7}} \right)}^n} + 1}}\]

\[ = \frac{{\lim \left[ {4.{{\left( {\frac{3}{7}} \right)}^n} + 7} \right]}}{{\lim \left[ {2.{{\left( {\frac{5}{7}} \right)}^n} + 1} \right]}} = \frac{{4.\lim {{\left( {\frac{5}{7}} \right)}^n} + \lim 7}}{{2\lim {{\left( {\frac{5}{7}} \right)}^n} + \lim 1}} = \frac{{4.0 + 7}}{{2.0 + 1}} = 7.\]

b) \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{\sqrt {{x^2} + 4x + 4} }}{{x + 2}}\)\( = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{{\sqrt {{{\left( {x + 2} \right)}^2}} }}{{x + 2}}\)\( = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{{\left| {x + 2} \right|}}{{x + 2}}\)\( = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{{x + 2}}{{x + 2}} = \mathop {\lim }\limits_{x \to - {2^ + }} 1 = 1.\)

(Vì \(x \to - {2^ + }\) thì \(\left| {x + 2} \right| > 0\) nên \(\left| {x + 2} \right| = x + 2\)).

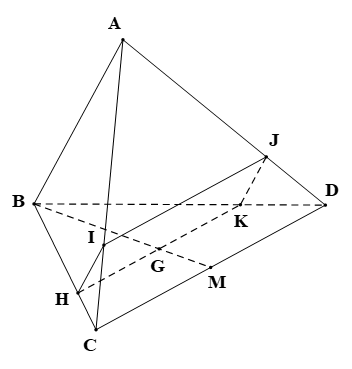
a) Gọi \(\Delta \) là giao tuyến của \(\left( P \right)\) và \(\left( {BCD} \right)\). Khi đó \(\Delta \) đi qua \(G\) và song song với \(CD.\)

Gọi \(H,\,\,K\) lần lượt là giao điểm của \(\Delta \) với \(BC\) và \(BD.\)

\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{H \in \left( P \right)}\\{H \in BC \subset \left( {BCD} \right)}\end{array}} \right. \Rightarrow H \in \left( P \right) \cap \left( {BCD} \right)(1)\]

\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{K \in \left( P \right)}\\{K \in BD \subset \left( {BCD} \right)}\end{array}} \right. \Rightarrow K \in \left( P \right) \cap \left( {BCD} \right)(2)\]

Từ \[\left( 1 \right),\left( 2 \right)\] ta có giao tuyến của \(\left( P \right)\) và \(\left( {BCD} \right)\) là \(HK.\)

b) Vì \(G\) là trọng tâm tam giác \(BCD\) và \(HK{\rm{//}}CD\) (do \[\Delta {\rm{//}}CD\]) nên theo định lí Thaés ta có: \(\frac{{CH}}{{CB}} = \frac{{MG}}{{MB}} = \frac{{DK}}{{DB}} = \frac{1}{3}\).

Giả sử \(\left( P \right)\) cắt hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {ABD} \right)\) lâng lượt tại các giao tuyến là \(HI\) và \(KJ.\)

Ta có \[\left( P \right) \cap \left( {ABC} \right) = HI\]; \[\left( P \right) \cap \left( {ABD} \right) = KJ\,.\]

Mà \[AB{\rm{//}}\left( P \right)\] và \[AB \subset \left( {ABC} \right);\,\,AB \subset \left( {ABD} \right)\] nên \[HI{\rm{//}}AB{\rm{//}}KJ.\]

Vì \(HI{\rm{//}}KJ\) nên bốn điểm \(H,\,\,I,\,\,K,\,\,J\) đồng phẳng.

Ta dễ dang có:

\[\left( P \right) \cap \left( {ABC} \right) = HI;\]

\(\left( P \right) \cap \left( {ACD} \right) = IJ;\)

\[\left( P \right) \cap \left( {ABD} \right) = KJ\,;\]

\[\left( P \right) \cap \left( {BCD} \right) = KH.\]

Như vậy, thiết diện của tứ diện \[ABCD\] cắt bởi mặt phẳng \[\left( P \right)\] là tứ giác \(HIJK.\)

Theo hệ quả định lí Thalès:

Trong tam giác \(ABC\) với \(HI{\rm{//}}AB\) ta có \(\frac{{HI}}{{AB}} = \frac{{CH}}{{CB}} = \frac{1}{3}.\)

Trong tam giác \(ABD\) với \(KJ{\rm{//}}AB\) ta có \(\frac{{KJ}}{{AB}} = \frac{{DK}}{{BD}} = \frac{1}{3}.\)

\( \Rightarrow \frac{{HI}}{{AB}} = \frac{{KJ}}{{AB}} = \frac{1}{3} \Rightarrow HI = KJ.\)

Xét tứ giác \(HIJK\) có: \(HI{\rm{//}}KJ\) và \(HI = KJ\) nên \(HIJK\) là hình bình hành.

Vậy thiết diện của \[\left( P \right)\] và tứ diện \[ABCD\] là hình bình hành \(HIJK\).