Cho biểu thức \(A = \frac{1}{{x\left( {x + 1} \right)}} + \frac{1}{{\left( {x + 1} \right)\left( {x + 2} \right)}} + \frac{1}{{x + 2}}\).
a) Tìm điều kiện xác định của biểu thức \(A.\)
b) Rút gọn biểu thức \(A\).
c) Tính giá trị của biểu thức \(A\) biết \(x\) thỏa mãn \(\left( {x - 2024} \right)\left( {x + 1} \right) = 0.\)
Cho biểu thức \(A = \frac{1}{{x\left( {x + 1} \right)}} + \frac{1}{{\left( {x + 1} \right)\left( {x + 2} \right)}} + \frac{1}{{x + 2}}\).
a) Tìm điều kiện xác định của biểu thức \(A.\)
b) Rút gọn biểu thức \(A\).
c) Tính giá trị của biểu thức \(A\) biết \(x\) thỏa mãn \(\left( {x - 2024} \right)\left( {x + 1} \right) = 0.\)
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
\(A = \frac{1}{{x\left( {x + 1} \right)}} + \frac{1}{{\left( {x + 1} \right)\left( {x + 2} \right)}} + \frac{1}{{x + 2}}\).
a) Điều kiện xác định của biểu thức \(A\) là: \(x \ne 0,\,\,x + 1 \ne 0,\,\,x + 2 \ne 0\) hay \(x \ne 0,\,\,x \ne - 1,\,\,x \ne - 2.\)
b) Với \(x \ne 0,\,\,x \ne - 1,\,\,x \ne - 2\) ta có:
\(A = \frac{1}{{x\left( {x + 1} \right)}} + \frac{1}{{\left( {x + 1} \right)\left( {x + 2} \right)}} + \frac{1}{{x + 2}}\)
\( = \frac{{\left( {x + 2} \right) + x + \left( {x + 1} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)
\( = \frac{{3x + 3}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)
\( = \frac{{3\left( {x + 1} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)
\( = \frac{3}{{x\left( {x + 2} \right)}}\).
Vậy với \(x \ne 0,\,\,x \ne - 1,\,\,x \ne - 2\) thì \(A = \frac{3}{{x\left( {x + 2} \right)}}.\)
c) Ta có: \(\left( {x - 2024} \right)\left( {x + 1} \right) = 0\)
Suy ra \(x - 2024 = 0\) (do \(x + 1 \ne 0)\)
Do đó \(x = 2024\) (thỏa mãn điều kiện)
Thay \(x = 2024\) vào biểu thức \(A\) ta được: \(A = \frac{3}{{2024 \cdot \left( {2024 + 2} \right)}} = \frac{3}{{2024 \cdot 2026}} = \frac{3}{{4\,\,100\,\,624}}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: C
Hình chóp tứ giác đều có 4 mặt bên, đều là các tam giác cân bằng nhau. Do đó diện tích xung quanh của hình chóp tứ giác đều bằng 4 lần diện tích một mặt bên.
Lời giải
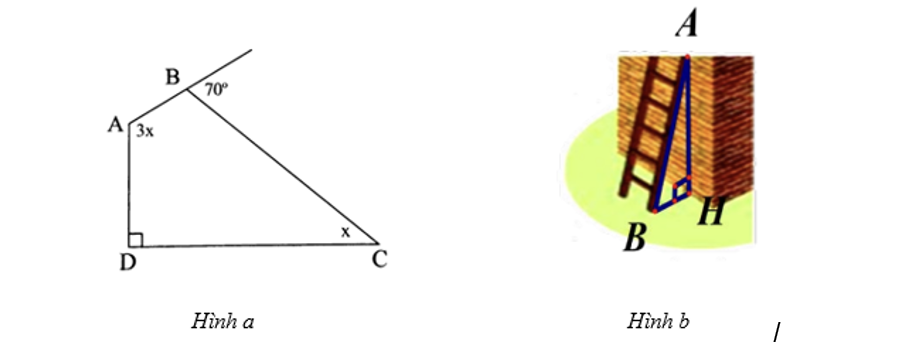
a) Góc ngoài tại đỉnh \(B\) có số đo bằng \(70^\circ \) nên góc trong tại đỉnh \(B\) có số đo bằng \(180^\circ - 70^\circ = 110^\circ \)
Xét tứ giác \(ABCD,\) ta có: \(\widehat {A\,\,} + \widehat {B\,} + \widehat {C\,} + \widehat {D\,} = 360^\circ \) (định lí tổng các góc của một tứ giác)
Do đó \(3x + 110^\circ + x + 90^\circ = 360^\circ \)
Suy ra \(4x = 160^\circ \) nên \(x = 40^\circ \)
Vậy \(x = 40^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.