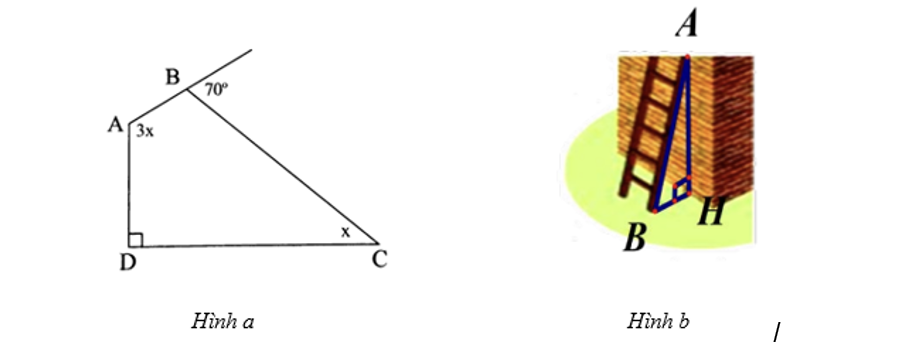
Một chiếc lều ở một trại hè của học sinh tham gia cắm trại có dạng hình chóp tứ giác đều theo các kích thước như hình vẽ bên.
a) Thể tích không khí bên trong lều là bao nhiêu (làm tròn kết quả đến chữ số thập phân thứ hai)?
b) Xác định số vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp, ...) là bao nhiêu (làm tròn kết quả đến chữ số thập phân thứ hai)? Biết độ dài trung đoạn của lều trại là \[2,24\] cm.
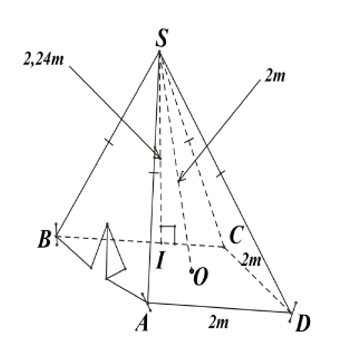
Một chiếc lều ở một trại hè của học sinh tham gia cắm trại có dạng hình chóp tứ giác đều theo các kích thước như hình vẽ bên.
a) Thể tích không khí bên trong lều là bao nhiêu (làm tròn kết quả đến chữ số thập phân thứ hai)?
b) Xác định số vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp, ...) là bao nhiêu (làm tròn kết quả đến chữ số thập phân thứ hai)? Biết độ dài trung đoạn của lều trại là \[2,24\] cm.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
a) Thể tích không khí bên trong lều chính là thể tích hình chóp tứ giác đều, và bằng:
\(V = \frac{1}{3}Sh = \frac{1}{3} \cdot {2^2} \cdot 2 = \frac{8}{3} \approx 2,67\) (m3).
b) Số mét vải bạt cần thiết để dựng lều chính là diện tích xung quanh hình chóp tứ giác đều, và bằng:
\({S_{xq}} = \frac{1}{2}Cd = \frac{1}{2}\left( {2 \cdot 4} \right) \cdot 2,24 = 8,96\) (m2).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\(A = \frac{1}{{x\left( {x + 1} \right)}} + \frac{1}{{\left( {x + 1} \right)\left( {x + 2} \right)}} + \frac{1}{{x + 2}}\).
a) Điều kiện xác định của biểu thức \(A\) là: \(x \ne 0,\,\,x + 1 \ne 0,\,\,x + 2 \ne 0\) hay \(x \ne 0,\,\,x \ne - 1,\,\,x \ne - 2.\)
b) Với \(x \ne 0,\,\,x \ne - 1,\,\,x \ne - 2\) ta có:
\(A = \frac{1}{{x\left( {x + 1} \right)}} + \frac{1}{{\left( {x + 1} \right)\left( {x + 2} \right)}} + \frac{1}{{x + 2}}\)
\( = \frac{{\left( {x + 2} \right) + x + \left( {x + 1} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)
\( = \frac{{3x + 3}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)
\( = \frac{{3\left( {x + 1} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)
\( = \frac{3}{{x\left( {x + 2} \right)}}\).
Vậy với \(x \ne 0,\,\,x \ne - 1,\,\,x \ne - 2\) thì \(A = \frac{3}{{x\left( {x + 2} \right)}}.\)
c) Ta có: \(\left( {x - 2024} \right)\left( {x + 1} \right) = 0\)
Suy ra \(x - 2024 = 0\) (do \(x + 1 \ne 0)\)
Do đó \(x = 2024\) (thỏa mãn điều kiện)
Thay \(x = 2024\) vào biểu thức \(A\) ta được: \(A = \frac{3}{{2024 \cdot \left( {2024 + 2} \right)}} = \frac{3}{{2024 \cdot 2026}} = \frac{3}{{4\,\,100\,\,624}}.\)
Câu 2
Lời giải
Đáp án đúng là: C
Hình chóp tứ giác đều có 4 mặt bên, đều là các tam giác cân bằng nhau. Do đó diện tích xung quanh của hình chóp tứ giác đều bằng 4 lần diện tích một mặt bên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.