(1,5 điểm) Chị Lan đã ghi lại khối lượng bán được của mỗi loại mà sạp hoa quả của chị bán được trong ngày và biểu diễn trong biểu đồ dưới đây:

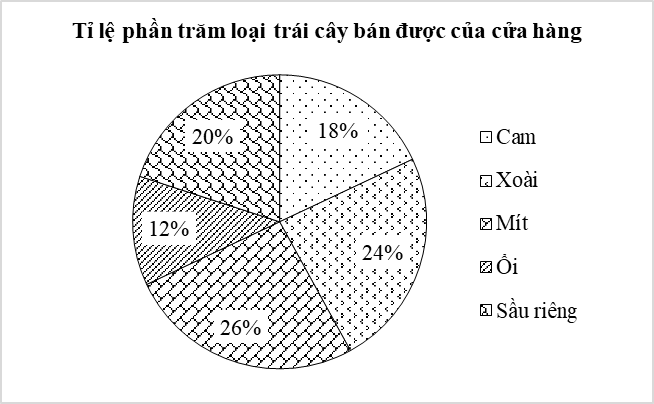
a) Chị Lan đã thu thập dữ liệu được biểu diễn trên biểu đồ bằng phương pháp thu thập trực tiếp hay gián tiếp?

b) Hãy chuyển đổi dữ liệu từ biểu đồ trên sang dạng bảng thống kê theo mẫu sau:

Loại trái cây	Tỉ lệ phần trăm
Cam	?
Xoài	?
Mít	?
Ổi	?
Sầu riêng	?

c) Cho biết chị Lan bán được tổng cộng 200 kg trái cây trong ngày hôm đó. Hãy tính số kilôgam sầu riêng mà sạp hoa quả của chị Lan đã bán được trong ngày ấy.

a) Xét tứ giác \[AHMK\] có:

\[\widehat {HAK} = 90^\circ \] (do \[\Delta ABC\] tại \[A,\,\,K \in AB,\,\,H \in AC);\]

\(\widehat {MHA} = 90^\circ \) (do \(MH \bot AC);\)

\[\widehat {MKA} = 90^\circ \] (do \[MK \bot AB)\]

Suy ra tứ giác \(AHMK\) là hình chữ nhật (dấu hiệu nhận biết).

b) Ta có \(AHMK\) là hình chữ nhật nên \(AM = HK\) và hai đường chéo này cắt nhau tại trung điểm \(I\) của mỗi đường.

Xét \(\Delta AMC\) có: \(I\) và \(D\) lần lượt là trung điểm của \(AM,MC\)

Suy ra \(ID\) là đường trung bình của \(\Delta AMC\)

Do đó \(ID\,{\rm{//}}\,AC\) và \(ID = \frac{1}{2}AC\) (tính chất đường trung bình của tam giác) (1)

Xét \(\Delta ABC\) có: \(M\) là trung điểm của \(BC\) và \(MH\,{\rm{//}}\,AB\) (cùng vuông góc \(AC)\)

Nên \(H\) là trung điểm của \(AC,\) do đó \(AH = \frac{1}{2}AC\) (2)

Từ (1) và (2) suy ra \(ID = AH.\)

Xét tứ giác \(AIDH\) có \(ID = AH\) (chứng minh trên) và \(ID\,{\rm{//}}\,AH\) (do \(ID\,{\rm{//}}\,AC)\)

Suy ra tứ giác \[AIDH\] là hình bình hành (dấu hiệu nhận biết).

c) ⦁ Xét \(\Delta KEH\) vuông tại \[E\] có \[I\] là trung điểm \[HK\] nên \[EI\] là đường trung tuyến ứng với cạnh huyền \[HK\]

Do đó \(EI = \frac{1}{2}HK\) (tính chất đường trung tuyến ứng với cạnh huyền).

Mà \(HK = AM\) (chứng minh ở câu b) nên \(EI = \frac{1}{2}AM\)

Mà \[I\] là trung điểm của \[AM\] nên \[EI\] là đường trung tuyến của \(\Delta AEM\)

Do đó \(\Delta AEM\) vuông tại \(E.\)

⦁ Ta có: \(EI = \frac{1}{2}AM\) và \(IM = \frac{1}{2}AM\) (do \(I\) là trung điểm của \(AM)\)

Do đó \(EI = IM,\) nên \(\Delta IME\) cân tại \(I,\) suy ra \(\widehat {{M_1}} = \widehat {{E_2}}\)

Mặt khác: \(\widehat {{M_1}} = \widehat {{E_1}}\) (hai góc so le trong do \(AM\,{\rm{//}}\,ED)\)

Nên \(\widehat {{E_1}} = \widehat {{E_2}}\) hay \[EM\] là phân giác \(\widehat {IEH}.\)

⦁ Vì \[AIDH\] là hình bình hành (câu b) nên \(AI\,{\rm{//}}\,HD\) hay \(AM\,{\rm{//}}\,ED\)

Do đó \(\widehat {{A_1}} = \widehat {{H_1}}\) (hai góc đồng vị)    (3)

Ta có \(AM = HK\) và \(AI = \frac{1}{2}AM,\) \(IH = \frac{1}{2}HK\) (do \(I\) là trung điểm của \(AM,HK)\)

Nên \(AI = IH,\) do đó \(\Delta AIH\) cân tại \(I\)

Suy ra \(\widehat {{A_1}} = \widehat {{H_2}}\) (4)

Từ (3) và (4) suy ra \(\widehat {{H_2}} = \widehat {{H_1}}\) hay \(HA\) là phân giác \[\widehat {EHI}.\]

⦁ Xét \[\Delta HIE\] có \[HA,\,\,EM\] lần lượt là phân giác \[\widehat {EHI}\] và \[\widehat {IEH}\]

Suy ra \(IN\) là phân giác \(\widehat {EIH}\) hay \(\widehat {{I_1}} = \widehat {{I_2}}.\)

Xét \(\Delta NIE\) và \(\Delta NIH\) có:

\[NI\] là cạnh chung;

\(\widehat {{I_1}} = \widehat {{I_2}}\)(chứng minh trên);

\(EI = IH\) (cùng bằng \(\frac{1}{2}AM)\)

Do đó \(\Delta NIE = \Delta NIH\) (c.g.c)

Suy ra \(NE = NH\) (hai cạnh tương ứng)

Nên \(\Delta NEH\) cân tại \[N\]

Do đó \(\widehat {NHE} = \widehat {NEH}\) (tính chất tam giác cân)

Mà \(AM\,{\rm{//}}\,ED\) nên \(\widehat {NHE} = \widehat {NMA}\) và \(\widehat {NEH} = \widehat {NAM}\) (các cặp góc đồng vị)   

Nên \(\widehat {NMA} = \widehat {NAM}\)    

Mặt khác, \(\widehat {NMA} = \widehat {MAB}\) (hai góc so le trong do \(MH\,{\rm{//}}\,AB)\)

Do đó, \(\widehat {NAM} = \widehat {MAB}\)

Vậy \(AM\) là phân giác của \(\widehat {NAB}.\)

Hướng dẫn giải

Đáp án đúng là: B

Xét \(\Delta ABC\) có \(AD\) là đường phân giác của góc \(BAC\) (do \(\widehat {BAD} = \widehat {CAD}),\) nên \(\frac{{AC}}{{AB}} = \frac{{DC}}{{DB}}\) (tính chất đường phân giác). Do đó \(\frac{y}{x} = \frac{9}{5}.\)