(2,5 điểm)
1. Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết \(1\,\,{\rm{inch}} \approx 2,54\,\,{\rm{cm}}\), điện thoại có chiều rộng là \[7\,\,{\rm{cm;}}\] chiều dài là \[15,5{\rm{ cm}}.\] Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch ? (Làm tròn kết quả đến hàng đơn vị).
2. Cho tam giác \(ABC\) nhọn có \(AB < AC\,.\) Gọi \(N\) là trung điểm của \(AC\,.\) Lấy điểm \(D\) trên tia \(BN\) sao cho \(BN = ND\,.\) Kẻ \(AP \bot BC\,,\,\,CQ \bot AD\,.\)
a) Chứng minh \(N\) là trung điểm của \(PQ\).
b) Tam giác \(ABC\) cần thêm điều kiện gì để tứ giác \(ABCD\) là hình vuông.
2. Cho tam giác \(ABC\) nhọn có \(AB < AC\,.\) Gọi \(N\) là trung điểm của \(AC\,.\) Lấy điểm \(D\) trên tia \(BN\) sao cho \(BN = ND\,.\) Kẻ \(AP \bot BC\,,\,\,CQ \bot AD\,.\)
a) Chứng minh \(N\) là trung điểm của \(PQ\).
b) Tam giác \(ABC\) cần thêm điều kiện gì để tứ giác \(ABCD\) là hình vuông.
Câu hỏi trong đề: Bộ 10 đề thi Cuối kì 1 Toán 8 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
1. Áp dụng định lí Pythagore vào tam giác \[ABC\] vuông tại \[A\], ta có:
\(B{C^2} = A{C^2} + A{B^2} = {\left( {15,5} \right)^2} + {7^2} = 289,25\)
Suy ra \[BC = \sqrt {289,25} \approx 17\,\,{\rm{(cm)}}\].
Vì \(1\,\,{\rm{inch}} \approx 2,54\,\,{\rm{cm}}\) nên chiếc điện thoại theo hình vẽ có: \(\frac{{17}}{{2,54}} \approx 7\,\,({\rm{inch)}}\)
Vậy chiếc điện thoại theo hình vẽ khoảng 7 inch.
2.
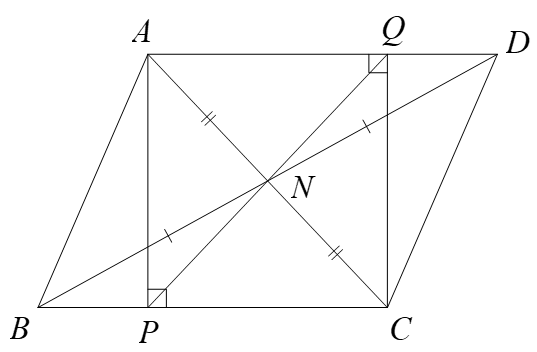
a) Ta có \(AP \bot BC;\,\,AQ\parallel BC\) suy ra \(AP \bot AQ\) hay \(\widehat {PAQ} = 90^\circ \).
Vì \(AP \bot BC\,,\,\,CQ \bot AD\,\) nên \(\widehat {APQ} = 90^\circ ;\,\,\widehat {AQC} = 90^\circ \).
Tứ giác \(APCQ\) có \(\widehat {PAQ} = 90^\circ \); \(\widehat {APQ} = 90^\circ ;\,\,\widehat {AQC} = 90^\circ \) nên là hình chữ nhật.
Khi đó hai đường chéo \(AC,\,\,PQ\) cắt nhau tại trung điểm của mỗi đường.
Mà \(N\) là trung điểm của \(AC\) nên \(N\) là trung điểm của \(PQ\).
b) Tứ giác \(ABCD\) có hai đường chéo \(AC,\,\,BD\) cắt nhau tại trung điểm \(N\) của mỗi đường nên là hình bình hành.
Để tứ giác \(ABCD\) là hình vuông thì ta cần \(AB \bot BC,\,\,AB = BC\) hay \(\Delta ABC\) vuông cân tại \(B\,.\)
Vậy để tứ giác \(ABCD\) là hình vuông thì tam giác \(ABC\) vuông cân tại \(B\,.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
a) Cửa hàng đã thu thập dữ liệu được biểu diễn trong biểu đồ trên bằng phương pháp phỏng vấn 1 000 khách hàng. Đây là phương pháp thu thập trực tiếp.
b) Hãy chuyển đổi dữ liệu từ biểu đồ trên sang dạng bảng thống kê theo mẫu sau:
|
Món ăn |
Tỉ lệ phần trăm |
|
Phở |
\[45\% \] |
|
Bún bò |
\[25\% \] |
|
Bánh mì |
\[18\% \] |
|
Gỏi cuốn |
\[12\% \] |
c) Nếu cửa hàng muốn kinh doanh một món ẩm thực duy nhất thì cửa hàng nên ưu tiên chọn món Phở. Vì đây là món ăn được khách hàng lựa chọn nhiều nhất (chiếm \[45\% ).\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Ta có \[{\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca\]
Theo bài, \[{\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2}\] nên suy ra \[ab + bc + ca = 0.\]
Đặt \[x = ab;y = bc;z = ca.\]
Khi đó \[x + y + z = 0.\] Suy ra \(x + y = - z;\,\,y + z = - x;\,\,z + x = - y.\)
Xét \[\left( {1 + \frac{a}{c}} \right)\left( {1 + \frac{b}{a}} \right)\left( {1 + \frac{c}{b}} \right)\]
\[ = \left( {1 + \frac{{ab}}{{bc}}} \right)\left( {1 + \frac{{bc}}{{ca}}} \right)\left( {1 + \frac{{ca}}{{ab}}} \right)\]
\[ = \left( {1 + \frac{x}{y}} \right)\left( {1 + \frac{y}{z}} \right)\left( {1 + \frac{z}{x}} \right)\]
\[ = \left( {\frac{{y + x}}{y}} \right)\left( {\frac{{z + y}}{z}} \right)\left( {\frac{{x + z}}{x}} \right)\]
\[ = \frac{{ - z}}{y}.\frac{{ - x}}{z}.\frac{{ - y}}{x} = - 1.\]
Xét \[\frac{{{a^3}{b^3} + {b^3}{c^3} + {c^3}{a^3}}}{{3{a^2}{b^2}{c^2}}}\]\[ = \frac{{{{\left( {ab} \right)}^3} + {{\left( {bc} \right)}^3} + {{\left( {ca} \right)}^3}}}{{3ab \cdot bc \cdot ca}}\]
\[ = \frac{{{x^3} + {y^3} + {z^3}}}{{3xyz}}\]\[ = \frac{{{{\left( {x + y} \right)}^3} - 3xy\left( {x + y} \right) + {z^3}}}{{3xyz}}\]
\[ = \frac{{{{\left( { - z} \right)}^3} - 3xy\left( { - z} \right) + {z^3}}}{{3xyz}}\]\[ = \frac{{ - {z^3} + 3xyz + {z^3}}}{{3xyz}} = \frac{{3xyz}}{{3xyz}} = 1.\]
Từ đó, \[T = \frac{{{a^3}{b^3} + {b^3}{c^3} + {c^3}{a^3}}}{{3{a^2}{b^2}{c^2}}} + \left( {1 + \frac{a}{c}} \right)\left( {1 + \frac{b}{a}} \right)\left( {1 + \frac{c}{b}} \right) = 1 + \left( { - 1} \right) = 0.\]
Vậy \(T = 0.\)
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập