(3,5 điểm)

1. Bạn Hà làm một cái lồng đèn hình quả trám (xem hình bên) là hình ghép từ hai hình chóp tứ giác đều có cạnh đáy \[20{\rm{ cm,}}\] cạnh bên \[26{\rm{ cm,}}\]khoảng cách giữa hai đỉnh của hai hình chóp là \[30{\rm{ cm}}.\]

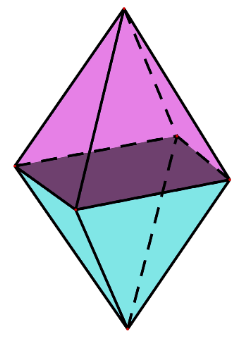
a) Tính thể tích của lòng đèn.

b) Bạn Hà muốn dán giấy mờ lên cái lòng đèn hình quả trám này thì cần phải chuẩn bị bao nhiêu mét vuông giấy (bỏ qua các mép dán)?

2. Cho tam giác \(ABC\) vuông ở \(A.\) Gọi \(G\) là trung điểm của \(BC.\) Qua \(G\) kẻ \(GE \bot AB\) \(\left( {E \in AB} \right)\) và \(GF \bot AC\) \(\left( {F \in AC} \right).\) Từ \(E\) kẻ đường thẳng song song với \(BF,\) đường thẳng này cắt \(GF\) tại \(I.\)

a) Chứng minh tứ giác \(BEIF\) là hình bình hành.

b) Tìm điều kiện của tam giác \(ABC\) để tứ giác \(AGCI\) là hình vuông.

Hướng dẫn giải

1.
a) Chiều cao của mỗi hình chóp tứ giác đều là \(30:2 = 15{\rm{\;}}\left( {{\rm{cm}}} \right).\)

Thể tích của lồng đèn quả trám là: \(V = 2 \cdot \left( {\frac{1}{3} \cdot {{20}^2} \cdot 15} \right) = 4\,\,000{\rm{\;}}\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)

Vậy thể tích của lòng đèn là \(4\,\,000{\rm{\;c}}{{\rm{m}}^3}.\)

b) Một nửa lồng đèn được mô tả bởi hình chóp \(S.ABCD\) với các kích thước như hình vẽ.

Gọi \(M\) là trung điểm của \(BC.\)

Do đó \(MB = MC = \frac{1}{2}BC = \frac{1}{2} \cdot 20 = 10{\rm{\;}}\left( {{\rm{cm}}} \right){\rm{.}}\)

Vì \(\Delta SBC\) cân tại \(S\) nên đường trung tuyến \(SM\) đồng thời là đường cao, do đó \(SM \bot BC\) nên \(\Delta SBM\) vuông tại \(M.\)

Áp dụng định lí Pythagore vào \(\Delta SBM\) vuông tại \(M,\) ta có:

\(S{B^2} = S{M^2} + M{B^2}\)

Suy ra \(S{M^2} = S{B^2} - M{B^2} = {26^2} - {10^2} = 676 - 100 = 576.\)

Do đó \[SM = 24{\rm{\;}}\left( {{\rm{cm}}} \right).\]

Diện tích xung quanh (diện tích 4 mặt bên) của hình chóp tứ giác đều là:

\({S_{xq}} = \frac{1}{2} \cdot \left( {4 \cdot 20} \right) \cdot 24 = 960{\rm{\;}}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)

Vậy diện tích giấy mờ bạn Hà cần chuẩn bị để làm lồng đèn hình quả trám đó là:

\(S = 2{S_{xq}} = 2 \cdot 960 = 1\,\,920{\rm{\;}}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)

2.

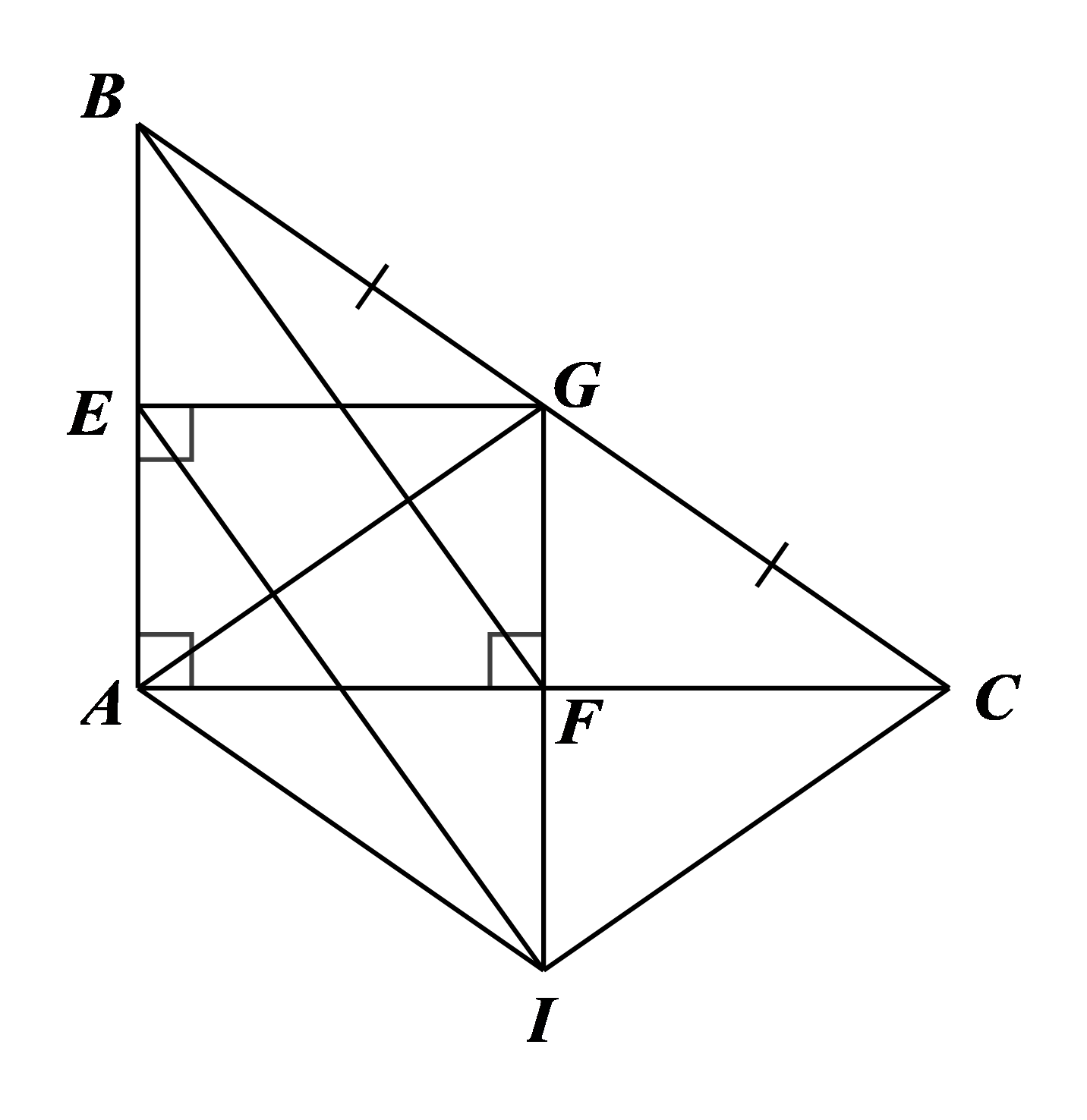
a) Ta có \(GF \bot AC\) và \(AB \bot AC\) (do \(\Delta ABC\) vuông tại \(A)\) nên \(GF\,{\rm{//}}\,AB.\)

Xét tứ giác \(BEIF\) có

\(BE\,{\rm{//}}\,FI\) (do \(GF\,{\rm{//}}\,AB)\) và \(EI\,{\rm{//}}\,BF\)

Do đó, tứ giác \(BEIF\) là hình bình hành.

b) Xét \(\Delta ABC\) vuông tại \(A\) có \(AG\) là đường trung tuyến ứng với cạnh huyền \(BC\) nên \(AG = \frac{1}{2}BC\) (tính chất đường trung tuyến ứng với cạnh huyền).

Mà \(G\) là trung điểm của \(BC\) nên \(BG = CG = \frac{1}{2}BC\).

Do đó \(AG = BG = CG = \frac{1}{2}BC.\)

Suy ra \(\Delta ABG\) và \(\Delta ACG\) đều là tam giác cân tại \(G.\)

Xét \(\Delta ABG\) cân tại \(G\) có đường cao \(GE\) nên đồng thời là đường trung tuyến, do đó \(E\) là trung điểm của \[AB\] nên \(BE = AE.\) (1)

Tương tự với \(\Delta ACG\) cân tại \(G\) ta cũng có \(GF\) vừa là đường cao đồng thời là đường trung tuyến nên \(F\) là trung điểm của \(AC.\)

Xét tứ giác \(AEGF\) có:

⦁ \(\widehat {EAF} = 90^\circ \) (do \(\Delta ABC\) vuông tại \(A);\)

⦁ \(\widehat {AEG} = 90^\circ \) (do \(GE \bot AB);\)

⦁ \(\widehat {AFG} = 90^\circ \) (do \(GF \bot AC)\).

Do đó tứ giác \(AEGF\) là hình chữ nhật.

Suy ra \(AE = GF\) (2)

Mà \(BEIF\) là hình bình hành nên \(BE = FI\) (3)

Từ (1), (2) và (3) suy ra \(GF = FI\) hay \(F\) là trung điểm của \(GI.\)

Xét tứ giác \(AGCI\) có hai đường chéo \(GI\) và \(AC\) cắt nhau tại trung điểm \(F\) của mỗi đường nên tứ giác \(AGCI\) là hình bình hành.

Lại có \(GI\) vuông góc với \(AC\) nên hình bình hành \(AGCI\) là hình thoi.

Để \(AGCI\) là hình vuông thì \(GI = AC\).

Lại có \(AB = 2AE,\,\,GI = 2GF\) và \(AE = GF\)nên \(AB = GI\).

Khi đó ta sẽ có \(AB = AC\) hay \(\Delta ABC\) cân tại \(A.\)

Vậy tam giác \(ABC\) vuông cân tại \(A\) thì \(AGCI\) là hình vuông.