Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
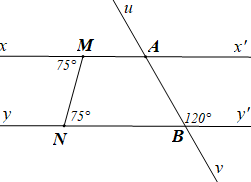
a) Học sinh vẽ lại hình theo đúng số đo các góc.
|
GT |
\(xx',\,\,yy',\,\,uv\) là các đường thẳng; Đoạn thẳng \(MN\) cắt \(xx'\) tại \(M\), \[\widehat {xMN} = 75^\circ \]; Đoạn thẳng \(MN\) cắt \(yy'\) tại \(N\), \[\widehat {MNy'} = 75^\circ \]; \(uv\) cắt \(xx'\) tại \(A\), \(uv\) cắt \(yy'\) tại \(B\), \(\widehat {ABy'} = 120^\circ \). c) tia \(At\) là tia phân giác của góc \(\widehat {MAB}\). |
|
KL |
b) Giải thích \(xx'\,{\rm{//}}\,yy'\). Tính \(\widehat {uAx'}\). c) Tính \(\widehat {MAt}\). |
b) Ta có \[\widehat {xMN} = \widehat {MNy'}\] (cùng bằng \[75^\circ \])
Mà hai góc này ở vị trí so le trong nên \(xx'\,{\rm{//}}\,yy'\) (dấu hiệu nhận biết).
Do \(xx'\,{\rm{//}}\,yy'\) suy ra \(\widehat {uAx'} = \widehat {ABy'} = 120^\circ \) (hai góc đồng vị).
c) Ta có \(\widehat {MAB} = \widehat {uAx'} = 120^\circ \) (hai góc đối đỉnh)
Vì tia \(At\) là tia phân giác của góc \(\widehat {MAB}\) nên \(\widehat {MAt} = \frac{1}{2}\widehat {MAB} = 60^\circ \).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: \(\frac{a}{c} = \frac{c}{b}\) suy ra \({c^2} = ab\).
Do đó: \(VT = \frac{{{a^2} + {c^2}}}{{{b^2} + {c^2}}}\)\( = \frac{{{a^2} + ab}}{{{b^2} + ab}}\)\( = \frac{{a.\left( {a + b} \right)}}{{b.\left( {a + b} \right)}}\)\( = \frac{a}{b}\)\( = VP\).
Vậy với \(a,b,c\) là các số khác \(0\) và \(a + b \ne 0\) thỏa mãn \(\frac{a}{c} = \frac{c}{b}\) thì \(\frac{{{a^2} + {c^2}}}{{{b^2} + {c^2}}} = \frac{a}{b}\).
Lời giải
Gọi \[a\], \(b\), \(c\) (quyển vở) lần lượt là số quyển vở lớp \(7A\), \(7B\), \(7C\) quyên góp được.
Theo đề, ta có tổng số quyển vở lớp \(7A\) và \(7B\) quyên góp được nhiều hơn lớp \(7C\) là 62 quyển, suy ra \(a + b - c = 62\).
Do số quyển vở mỗi lớp quyên góp được tỉ lệ thuận với số học sinh của lớp đó nên:
\(\frac{a}{{32}} = \frac{b}{{35}} = \frac{c}{{36}}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{a}{{32}} = \frac{b}{{35}} = \frac{c}{{36}} = \frac{{a + b - c}}{{32 + 35 - 36}} = \frac{{62}}{{31}} = 2\).
Suy ra \(a = 32.2 = 64\); \(b = 35.2 = 70\); \(c = 36.2 = 72\).
Vậy số quyển vở lớp \(7A\), \(7B\), \(7C\) quyên góp được lần lượt là 64 quyển vở; 70 quyển vở và 72 quyển vở.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập