Một hình lăng trụ đứng có đáy là tam giác đều, chiều cao hình lăng trụ bằng \[10\,\,{\rm{cm,}}\] diện tích xung quanh của hình lăng trụ đứng bằng \[120\,\,{\rm{c}}{{\rm{m}}^2}\]. Độ dài cạnh đáy của hình lăng trụ đứng đó là        

Gọi \(x,y\,\,\left( {\rm{g}} \right)\) lần lượt là khối lượng của thanh kim loại thứ nhất và thanh kim loại thứ hai.

Thanh thứ hai nặng hơn thanh thứ nhất \(15,6\,\,{\rm{g}}\) nên \(y - x = 15,6\).

Vì hai thanh kim loại đồng chất nên khối lượng và thể tích của mỗi thanh kim loại là hai đại lượng tỉ lệ thuận. Do đó, ta có \(\frac{x}{5} = \frac{y}{7}\).

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\frac{x}{5} = \frac{y}{7} = \frac{{y - x}}{{7 - 5}} = \frac{{15,6}}{2} = 7,8\).

Suy ra \(x = 7.8.5 = 39\); \(y = 7,8.7 = 54,6\).

Vậy khối lượng của thanh kim loại thứ nhất và thanh kim loại thứ hai lần lượt là \(39\,\,{\rm{g}}\) và \(54,6\,\,{\rm{g}}\).

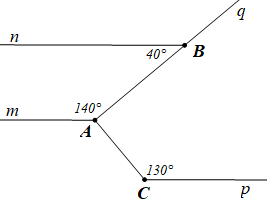
a) Học sinh vẽ lại hình theo đúng số đo các góc.

b) Ta có \(\widehat {ABn} + \widehat {nBq} = 180^\circ \) (hai góc kề bù)

Suy ra \(\widehat {nBq} = 180^\circ - \widehat {ABn} = 180^\circ - 40^\circ = 140^\circ \)

Do đó \(\widehat {BAm} = \widehat {nBq}\) (cùng bằng \(140^\circ \))

Mà hai góc này ở vị trí đồng vị

Do đó \(Am\,{\rm{//}}\,Bn\) (dấu hiệu nhận biết).

c) Ta có \(Am\,{\rm{//}}\,Bn\) (câu b) và \(Bn\,{\rm{//}}\,Cp\) (giả thiết)

Do đó \(Am\,{\rm{//}}\,Cp\).

Suy ra \(\widehat {ACp} = \widehat {CAm} = 130^\circ \) (so le trong).

Ta có \(\widehat {BAm} + \widehat {CAm} + \widehat {BAC} = 360^\circ \).

Vậy \(\widehat {BAC} = 360^\circ - \widehat {BAm} - \widehat {CAm} = 90^\circ \).

d) Ta có \(\widehat {ACp} = \widehat {ACr} + \widehat {rCp}\)

Suy ra \(\widehat {ACr} = \widehat {ACp} - \widehat {rCp} = 130^\circ - 40^\circ = 90^\circ \)

Hay \(AC \bot Cr\)

Mà \(\widehat {BAC} = 90^\circ \) (câu c) hay\(AC \bot Aq\).

Do đó \(Cr\,{\rm{//}}\,Aq\).