(2,0 điểm) Cho hình vẽ sau:

a) Chứng minh rằng \(TF\parallel EC\).
b) Từ \(TF\parallel EC\) tính \(\widehat {FEQ}\).
(2,0 điểm) Cho hình vẽ sau:

a) Chứng minh rằng \(TF\parallel EC\).
b) Từ \(TF\parallel EC\) tính \(\widehat {FEQ}\).
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
a) Ta có \(\widehat {TFQ} = 80^\circ + 20^\circ = 100^\circ \).
Vì \({\widehat F_1}\) và \(\widehat {TFQ}\) là hai góc kề bù nên \({\widehat F_1} + \widehat {TFQ} = 180^\circ \).
Suy ra \({\widehat F_1} = 180^\circ - \widehat {TFQ} = 180^\circ - 100^\circ = 80^\circ \).
Khi đó ta có \(\widehat {{F_1}} = \widehat {FQE} = 80^\circ \).
Mà \(\widehat {{F_1}}\) và \(\widehat {FQE}\) ở vị trí đồng vị trong
Do đó \(TF\parallel EC\).
b) Ta thấy \(\widehat {FEQ}\) và \(\widehat {TFE}\)nằm ở vị trí so le trong.
Mà theo a) ta có: \(TF\parallel EC\) nên suy ra.
\(\widehat {FEQ} = \widehat {TFE} = 80^\circ \).
Vậy \(\widehat {FEQ} = 80^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
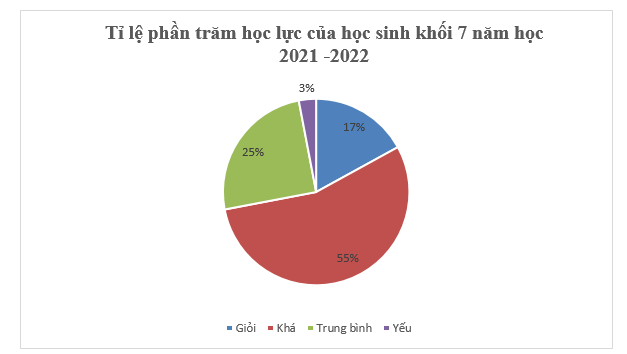
a) Biểu đồ đã cho là biểu đồ hình quạt tròn.
b) Tỉ lệ phần trăm số học sinh đạt học lực khá và trung bình lần lượt là 55% và 25%.
Tỉ lệ phần trăm số học sinh đạt học lực khá lớn hơn tỉ lệ phần trăm số học sinh đạt học lực trung bình là:
\(55\% - 25\% = 30\% \).
Vậy tỉ lệ phần trăm số học sinh đạt học lực khá lớn hơn tỉ lệ phần trăm số học sinh đạt học lực trung bình là 30%.
Lời giải
Ta có \(B = \frac{{2021}}{1} + \frac{{2020}}{2} + \frac{{2019}}{3} + ... + \frac{2}{{2020}} + \frac{1}{{2021}}\)
\( = 1 + \left( {\frac{{2020}}{2} + 1} \right) + \left( {\frac{{2019}}{3} + 1} \right) + \left( {\frac{{2018}}{4} + 1} \right) + ... + \left( {\frac{2}{{2020}} + 1} \right) + \left( {\frac{1}{{2021}} + 1} \right)\)
\( = 1 + \frac{{2020 + 2}}{2} + \frac{{2019 + 3}}{3} + ... + \frac{{2 + 2020}}{{2020}} + \frac{{1 + 2021}}{{2021}}\)
\( = \frac{{2022}}{{2022}} + \frac{{2022}}{2} + \frac{{2022}}{3} + ... + \frac{{2022}}{{2022}} + \frac{{2022}}{{2021}}\)
\( = 2022\left( {\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{{2020}} + \frac{1}{{2021}} + \frac{1}{{2022}}} \right) = 2022A\).
Vậy \(\frac{A}{B} = \frac{A}{{2022A}} = \frac{1}{{2022}}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

