Một công ty du lịch thông báo giá tiền cho chuyến đi tham quan của một nhóm khách du lịch như sau: 50 khách đầu tiên có giá là 3 000 000 đồng/người. Nếu có nhiều hơn 50 người đăng kí thì cứ có thêm 1 người, giá chuyến du lịch sẽ giảm 50 000 đồng/người cho toàn bộ hành khách. Để đạt doanh thu cao nhất thì công ty cần đón đoàn khách (nhiều hơn 50 khách) bao nhiêu người?
Một công ty du lịch thông báo giá tiền cho chuyến đi tham quan của một nhóm khách du lịch như sau: 50 khách đầu tiên có giá là 3 000 000 đồng/người. Nếu có nhiều hơn 50 người đăng kí thì cứ có thêm 1 người, giá chuyến du lịch sẽ giảm 50 000 đồng/người cho toàn bộ hành khách. Để đạt doanh thu cao nhất thì công ty cần đón đoàn khách (nhiều hơn 50 khách) bao nhiêu người?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \(x\) là số lượng khách thứ 51 trở lên, \(x > 0,\,\,x \in \mathbb{N}.\)
Cứ thêm một người thì giá chuyến du lịch còn lại là: \[300\,\,0000 - 50\,\,000 \cdot 1\] đồng/ người cho toàn bộ hành khách.
Thêm \(x\) người thì giá chuyến du lịch còn lại là: \[300\,\,0000 - 50\,\,000x\] đồng/người cho toàn bộ hành khách.
Doanh thu công ty du lịch thu được là:
\(T = \left( {50 + x} \right)\left( {3\,\,000\,\,000 - 50\,\,000x} \right) = 50\,\,000\left( {50 + x} \right)\left( {60 - x} \right)\) (đồng).
Để doanh thu cao nhất thì ta tìm giá trị lớn nhất của biểu thức \(T.\)
⦁ Chứng minh bất đẳng thức: \(ab \le {\left( {\frac{{a + b}}{2}} \right)^2}\,\,\,\,\left( * \right)\) với \(a,\,\,b\) là các số không âm.
Thật vậy, xét hiệu \({\left( {\frac{{a + b}}{2}} \right)^2} - ab = \frac{{{a^2} + 2ab + {b^2} - 4ab}}{4} = \frac{{{a^2} - 2ab + {b^2}}}{4} = \frac{{{{\left( {a - b} \right)}^2}}}{2}\)
Với mọi \(a,\,\,b\) là các số không âm, ta có:
\({\left( {a - b} \right)^2} \ge 0\) nên \(\frac{{{{\left( {a - b} \right)}^2}}}{2} \ge 0\) suy ra \({\left( {\frac{{a + b}}{2}} \right)^2} \ge ab\).
Dấu “=” xảy ra khi và chỉ khi \(a = b.\) Như vậy bất đẳng thức \(\left( * \right)\) đã được chứng minh.
⦁ Áp dụng bất đẳng thức \(\left( * \right)\) vào biểu thức \(T = 50\,\,000\left( {50 + x} \right)\left( {60 - x} \right),\) ta được:
\[T = 50\,\,000\left( {50 + x} \right)\left( {60 - x} \right) \le 50\,\,000 \cdot {\left( {\frac{{50 + x + 60 - x}}{2}} \right)^2} = 151\,\,250\,\,000\].
Dấu “=” xảy ra khi và chỉ khi \[50 + x = 60 - x\] hay \[x = 5\].
Vậy nếu đoàn khách có \(50 + 5 = 55\) người thì công ty du lịch đạt doanh thu cao nhất là \[151\,\,250\,\,000\] đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
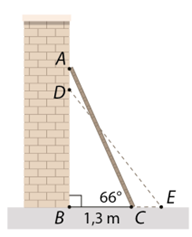
Xét \(\Delta ABC\) vuông tại \(A,\) ta có:
\(BC = AC \cdot \cos C\), suy ra \(AC = \frac{{BC}}{{\cos C}} = \frac{{1,3}}{{\cos 66^\circ }} \approx 3,20\) (m).
Xét \(\Delta ABC\) vuông tại \(A,\) ta có: \(AB = BC \cdot \tan C = 1,3 \cdot \tan 66^\circ \approx 2,92\) (m).
Khi đầu \(A\) của thang bị trượt xuống \(40{\rm{\;cm}} = 0,4{\rm{\;m}}\) đến vị trí \(D\) thì \(DB = AB - AD \approx 2,92 - 0,4 = 2,52\) (m) và chiều dài thang là \(DE = AC \approx 3,20\) (m).
Xét \(\Delta BDE\) vuông tại \(B,\) ta có:
\(\sin \widehat {DEB} = \frac{{BD}}{{DE}} \approx \frac{{2,52}}{{3,2}} = 0,7875\), suy ra \(\widehat {DEB} \approx 51^\circ 57'.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) \(\left( { - 2x + 5} \right)\left( {\frac{3}{4}x - 6} \right) = 0\)
\( - 2x + 5 = 0\) hoặc \(\frac{3}{4}x - 6 = 0\)
\( - 2x = - 5\) hoặc \(\frac{3}{4}x = 6\)
\(x = \frac{5}{2}\) hoặc \(x = 8\)
Vậy phương trình đã cho có hai nghiệm là \(x = \frac{5}{2};\) \(x = 8\).b) Điều kiện xác định: \(x \ne 2,\,\,x \ne - 2.\)
\(\frac{{x + 2}}{{x - 2}} = \frac{{x - 2}}{{x + 2}} + \frac{{16}}{{{x^2} - 4}}\)
\(\frac{{{{\left( {x + 2} \right)}^2}}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} = \frac{{{{\left( {x - 2} \right)}^2}}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} + \frac{{16}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\({\left( {x + 2} \right)^2} = {\left( {x - 2} \right)^2} + 16\)
\({x^2} + 4x + 4 = {x^2} - 4x + 4 + 16\)
\(8x = 16\)
\(x = 2\) (không thỏa mãn điều kiện)
Vậy phương trình đã cho vô nghiệm.Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập