Bạn Nam thực hiện trang trí một bức tường của lớp học bằng cách vẽ lên bức tường đó \[n\] đường tròn đồng tâm \[O\] với \(n \in \mathbb{N}*\). Biết rằng đường tròn thứ nhất \[\left( {O;\,{r_1}} \right)\] có đường kính bằng \[4\left( {cm} \right)\], mỗi đường tròn sau có chu vi bằng 2 lần chu vi của đường tròn kề ngay trước đó và chu vi đường tròn thứ \[n\] gấp 256 lần chu vi đường tròn thứ nhất. Tính bán kính của đường tròn thứ \[n - 2\].

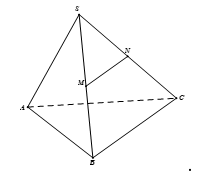
Cho hình chóp \(S.ABC\). Gọi \(M,\,N\) lần lượt là trung điểm của các cạnh \(SB,\,SC\). Trong các khẳng định sau, khẳng định nào đúng?

Cho hình hộp \(ABCD.A'B'C'D'\). Hình chiếu của điểm \[B'\] lên mặt phẳng \(\left( {ABCD} \right)\) theo phương chiếu \[AA'\] là

Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành tâm \[O\].

a) Tìm giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right)\].

b) Gọi \[G\] là trọng tâm tam giác \[SBD\], trên cạnh \[CD\] lấy điểm \[M\] sao cho \[DM = 2MC\].

Chứng minh: \[GM\parallel \left( {SBC} \right)\].

Cho dãy số \[\left( {{u_n}} \right)\] có \[\mathop {\lim }\limits_{n \to + \infty } {u_n} = 3\], dãy số \[\left( {{v_n}} \right)\] có \[\mathop {\lim }\limits_{n \to + \infty } {v_n} = 5\]. Giá trị \[\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n}.{v_n}} \right)\] bằng

Cho hình hộp \(ABCD.A'B'C'D'\). Hình chiếu của \(\Delta A'B'C'\) lên mặt phẳng \(\left( {ABCD} \right)\) theo phương chiếu \[AA'\] là

Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = 3n - 2\). Ba số hạng đầu tiên của dãy số \(\left( {{u_n}} \right)\) lần lượt là