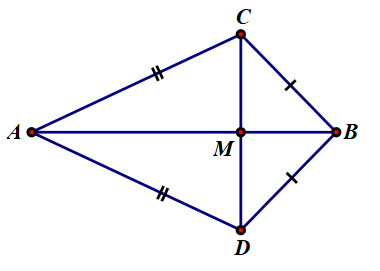
Cho hình vẽ bên, biết \[AC = AD,BC = BD\] và \[M\] là giao điểm của \[AB\] và \[CD.\]

Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: a) S b) Đ c) Đ d) Đ
• Xét \[\Delta ABC\] và \[\Delta ADB\], có:
\[AC = AD\] (gt)
\[BC = BD\] (gt)
\[AB\] chung (gt)
Do đó \[\Delta ABC = \Delta ABD\] (c.c.c)
Vậy ý a) là sai.
• Vì \[\Delta ABC = \Delta ABD\] (c.c.c) nên \[\widehat {BAC} = \widehat {BAD}\] (hai góc tương ứng).
Mà tia \[AB\] nằm giữa hai tia \[AC\] và \[AD\] nên \[AB\] là phân giác của \[\widehat {CAD}.\] Vậy ý b) là đúng.
• Xét \[\Delta ACM\] và \[\Delta ADM\] có:
\[AC = AD\] (gt)
\[\widehat {BAC} = \widehat {BAD}\](cmt)
\[AM\] chung (gt)
Nên \[\Delta ACM = \Delta ADM\] (c.g.c). Do đó, ý c) là đúng.
• Vì \[\Delta ACM = \Delta ADM\] (cmt) nên \[\widehat {AMC} = \widehat {AMD}\] (hai góc tương ứng).
Mà \[\widehat {AMC},\widehat {AMD}\] là hai góc kề bù nên \[\widehat {AMC} + \widehat {AMD} = 180^\circ \] hay \[\widehat {AMC} = \widehat {AMD} = 90^\circ \].
Do đó, \[AM \bot CD\] hay \[AB \bot CD\]. Vậy ý d) là đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Lời giải: 100
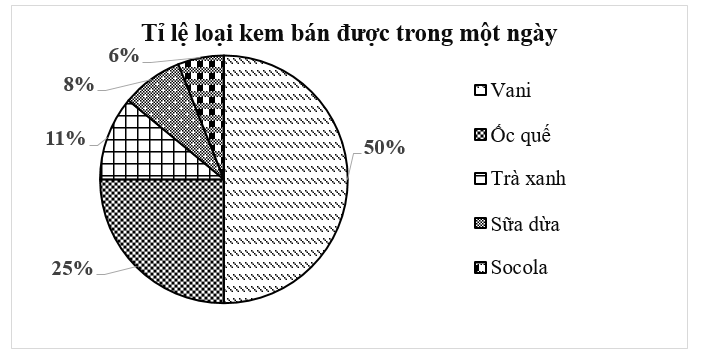
Nhận thấy, số kem vani bán được trong một ngày của cửa hàng chiếm \[50\% \] .
Do đó, số kem vani của cửa hàng bán được trong một ngày của cửa hàng là:
\[200 \cdot 50\% = 100\] (cây kem).
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đ b) S c) S d) Đ
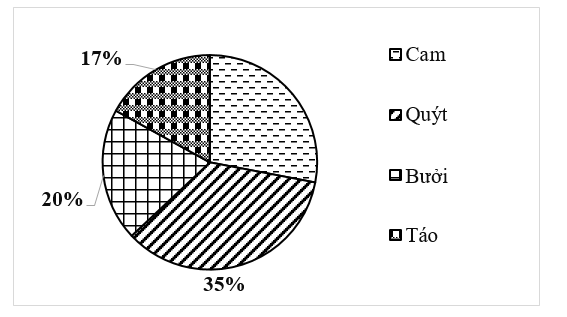
• Lượng cam tiêu thụ chiếm số phần trăm là: \[100\% - \left( {35\% + 20\% + 17\% } \right) = 28\% \]. Do đó, ý a) là đúng.
• Hai loại quả có lượng tiêu thụ nhiều nhất là quýt (35%) và cam (28%). Do đó, ý b) là sai.
• Tổng tỉ lệ lượng cam và lượng bưởi bán được là: \[35\% + 28\% = 63\% \]. Do đó, ý c) là sai.
• Tổng khối lượng hoa quả bán được của cửa hàng trong ngày hôm đó là: \[\left( {189:28} \right) \cdot 100 = 675\] (kg).
Vậy ý d) là đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.