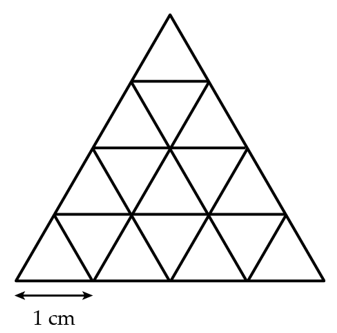
Cho hình vẽ bên.
a) Có bao nhiêu hình tam giác được cấu tạo bởi các hình tam giác có cạnh là 1 cm?
b) Xóa 2 đoạn 1 cm để được ít hình tam giác nhất.
Cho hình vẽ bên.
a) Có bao nhiêu hình tam giác được cấu tạo bởi các hình tam giác có cạnh là 1 cm?
b) Xóa 2 đoạn 1 cm để được ít hình tam giác nhất.

Quảng cáo
Trả lời:
a) Có số tam giác được cấu tạo bởi các hình tam giác có cạnh là 1 cm là:
1 + 3 + 5 + 7 = 16 (hình tam giác)
b) Xóa hai đoạn thuộc đường chéo hoặc trung tâm của hình sẽ làm mất nhiều tam giác nhất.
Ví dụ như sau:
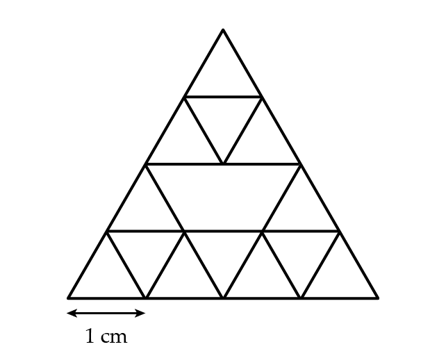
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
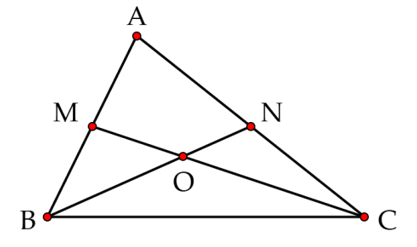
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 120 cm2.
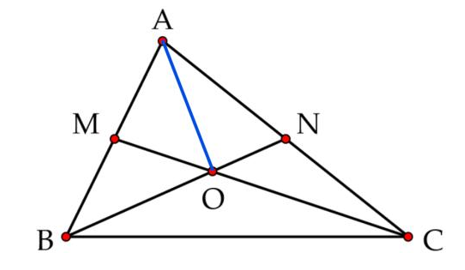
Nối A với O.
Vì M là trung điểm của AB nên AM = MB = \(\frac{1}{2}\)AB Suy ra:
\({S_{BMO}} = \frac{1}{2} \times {S_{ABO}}\) (Chung chiều cao từ O) nên \({S_{ABO}} = 20c{m^2} \times 2 = 40c{m^2}\)
\({S_{BMO}} = {S_{AMO}}\) (Chung chiều cao từ O)
\({S_{BCM}} = {S_{ACM}}\) (Chung chiều cao từ O)
Suy ra \({S_{BCM}} - {S_{BMO}} = {S_{ACM}} - {S_{AMO}}\)hay \({S_{BCO}} = {S_{ACO}} = 40c{m^2}\)
Vì N là trung điểm của AC nên AN = NC =\(\frac{1}{2}\) ACx . Suy ra:
\({S_{AON}} = {S_{CON}}\)(Chung chiều cao từ O)
\({S_{ABN}} = {S_{ACM}}\) (Chung chiều cao từ O)
Suy ra \({S_{ABN}} - {S_{AON}} = {S_{ACM}} - {S_{CON}}\)hay \({S_{ABO}} = {S_{BOC}} = 40c{m^2}\)
Diện tích tam giác ABC là: 40 + 40 + 40 = 120 (cm2)
Lời giải
Đáp án: 40,035 cm2
Hướng dẫn:
Bán kính hình tròn lớn là: 10 : 2 = 5 (cm)
Bán kính hình tròn bé là: 7 : 2 = 3,5 (cm)
Diện tích phần tô đậm là: 5 × 5 × 3,14 – 3,5 × 3,5 × 3,14 = 40,035 (cm2)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.