Trong giờ trả bài, cô giáo đã chuẩn bị \(40\) phiếu đại diện số thứ tự của từng học sinh trong lớp. Cô chọn ngẫu nhiên một phiếu. Tính xác suất của biến cố “Phiếu chọn được là phiếu có một chữ số \(2\) và có đúng hai ước”. (Kết quả ghi dưới dạng số thập phân)

Hướng dẫn giải

Lời giải: 100

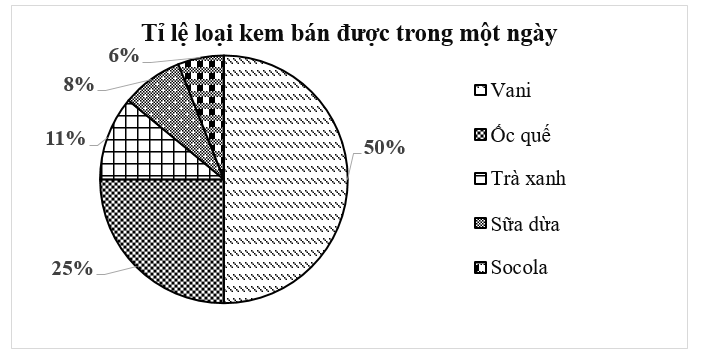
Nhận thấy, số kem vani bán được trong một ngày của cửa hàng chiếm \[50\% \] .

Do đó, số kem vani của cửa hàng bán được trong một ngày của cửa hàng là:

\[200 \cdot 50\% = 100\] (cây kem).

Hướng dẫn giải

Đáp án đúng là: a) Đ                             b) S                         c) S            d) Đ

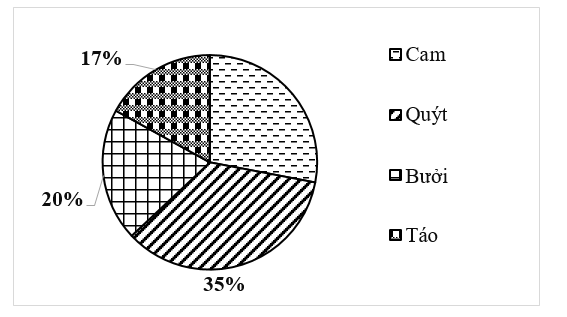
• Lượng cam tiêu thụ chiếm số phần trăm là: \[100\% - \left( {35\% + 20\% + 17\% } \right) = 28\% \]. Do đó, ý a) là đúng.

• Hai loại quả có lượng tiêu thụ nhiều nhất là quýt (35%) và cam (28%). Do đó, ý b) là sai.

• Tổng tỉ lệ lượng cam và lượng bưởi bán được là: \[35\% + 28\% = 63\% \]. Do đó, ý c) là sai.

• Tổng khối lượng hoa quả bán được của cửa hàng trong ngày hôm đó là: \[\left( {189:28} \right) \cdot 100 = 675\] (kg).

Vậy ý d) là đúng.